(иллюстрации к расчету p-value)
Как рассчитывал
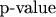
писал ранее:
1. По определению

- вероятность, что статистика (в данном случае - количество умерших, при известном количестве заболевших и при оцененном коэффициенте смертности) имеет наблюдаемой значение или более экстремальное.
2. Рассчитывалось (Экселем

)

, где

- вероятность, что значение количества умерших будет таким же, как наблюдается (

) или меньше.

- функция распределения вероятности для биноминального распределения.
3. Рассчитывалось


- вероятность, что значение количества умерших будет таким же, как наблюдается (

) или больше.

- вероятность того, что значение будет ровно таким, как наблюдается. Так как распределение дискретное, эту поправку нужно учитывать.
4. Рассчитывалось
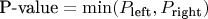
Ниже две картинки (примеры для расчета для двух провинций) для иллюстрации


Нужно обратить внимание, что вероятность возникновения наблюдаемого значения ("P_center", выделено красным цветом) считается, как в левом "хвосте", так и в правом. Это особенность дискретного распределения, с непрерывным таких сложностей нет. Остальное, вроде бы, понятно из текста выше и картинок.
Если что - спрашивайте.
Спрятал в офф-топик, чтобы не загромождать тему.
(в предположении что

везде достаточно велико для применения терминов нормального распределения):
Это излишне оптимистичное предположение. Для биномиального распределения при

:
а) только с

мода становится больше нуля.
б) при

в несколько сотен мода отлична от нуля, но "колокол" визуально весьма асимметричен
Однако, не смотря на это, Вы пришли к тем же выводам, что и я в пункте 5:
Половина провинций не попали в одну сигму (должны были попасть

или 20шт, на
5 больше),
Болд-мой
8шт вылезло за 2 сигмы (вместо 1-2шт)
То есть 6-7 штук "лишних" "вылезло за 2 сигмы"
5шт улетели за 3 сигмы,
Болд-мой
То есть 5-7 семь штук имеют столь малую вероятность, что принять нулевую гипотезу (распределение везде биномиальное с

) не можем.
Тоже самое получилось и у меня "в пятом пункте", если использовать поправку на множественность гипотез по Бенджамини — Хохбергу
в) Шесть строчек не проходят тест с поправкой по Бенджамини — Хохбергу
Т.е. или распределение не биноминально, и/или центр не на

.
Мы можем попытаться "подвигать центр", но избавиться от "невероятных" случаев не сможем. Сможем уменьшить их количество, например до 3-4, но вероятность оставшихся станет еще меньше. Что я и попытался сделать в пункте 6.
То есть:
а) либо распределение не биномиальное.
б) либо биномиальное, но параметр распределения

(то есть коэффициент летальности) таки разный в разных провинциях.



