Квазипростые числа

[khasanov.sm]

Добрый день!

Помогите пожалуйста со следующей задачей на индукцию:

Рассмотрим подмножество натуральных чисел S:

$S = \left\lbrace 4k+1 | k =0,1,...\right\rbrace$

Индукцией по $n \in S$ показать, что существует разложение $n = q_1 \cdot q_2...\cdot q_t$, где $q_i$ - далее неразложимые элементы из S.

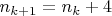
Предположение индукции. Разложение справедливо для k элемента множества: $n_k = q_1 \cdot q_2...\cdot q_t$. Мне понятно, что для следующего k+1 элемента будет справедлива формула: $n_{k+1} = n_k +4$. Так как множители в разложении являются элементами из S, то получим следующую формулу для k+1 элемента:$n = q_1 \cdot q_2 \cdot...q_{i-1}\cdot(4k_i+1)\cdot q_{i+1}...\cdot q_t + 4$, что позволит разложить k+1 элемент в сумму 4 элементов, которые по предположению индукции раскладываются в произведение неразложимых элементов.

Другие мысли не приходят на ум, а задачку решить охото.

[mihaild]

khasanov.sm в сообщении #1442873 писал(а):

:$n = q_1 \cdot q_2 \cdot...q_{i-1}\cdot(4k_i+1)\cdot q_{i+1}...\cdot q_t + 4$, что позволит разложить k+1 элемент в сумму 4 элементов

Что-то совсем невнятное написано. Что такое $n$, что такое $i$, откуда взялась сумма?

И что такое "далее неразложимые" - не представляющиеся в виде нетривиального произведения элементов из $S$?

Если да, то схема доказательства такая: пусть элементы вплоть до $k$-го разложимы. Тогда $k+1$-й элемент либо делится на один из предыдущих, либо не делится. Во втором случае всё понятно, в первом нужно доказать его разложимость.

[nnosipov]

khasanov.sm
Здесь лучше использовать другую схему рассуждения по индукции: пусть утверждение доказано для всех чисел из $S$, меньших $n$; докажем утверждение для числа $n$.

khasanov.sm в сообщении #1442873 писал(а):

Мне понятно, что для следующего k+1 элемента будет справедлива формула: $n_{k+1} = n_k +4$. Так как множители в разложении являются элементами из S, то получим следующую формулу для k+1 элемента:
$n = q_1 \cdot q_2 \cdot...q_{i-1}\cdot q_{i+1}...\cdot q_t$,

Это какая-то ерунда написана.

Вообще, утверждение о возможности разложения на неразложимые элементы (какой-либо природы) обычно бывает более-менее очевидно (классический пример: разложение натуральных чисел в произведение простых чисел). А проблемы бывают с доказательством единственности такого разложения. Вот в этом хорошо известном примере Гильберта (множество $S$) ее как раз и нет.

-- Ср мар 04, 2020 19:30:59 --

mihaild в сообщении #1442876 писал(а):

Тогда $k+1$-й элемент либо делится на один из предыдущих, либо не делится. Во втором случае всё понятно, в первом нужно доказать его разложимость.

Усложняете, всё проще.
Upd. Хотя нет, это то же самое, только другими словами. Самое трудное --- это обсуждать банальности.

[B@R5uk]

khasanov.sm, вот вы рассматриваете элементы вашего множества в порядке возрастания, и у вас каждый следующий элемент либо делится на какой-то предыдущий, либо не делится. В первом случае требуемое по условию разложение представляет лишь сам рассматриваемый элемент. А во втором — задача сводится к комбинированию двух уже решённых.

[B@R5uk]

khasanov.sm, посмотрите Соросовский образовательный журнал 2000 год, номер 3, том 6, раздел "Математика", статья В.В. Жикова "Основная теорема арифметики". Там на странице 113 как раз приводится искомое вами доказательство для натуральных чисел и для вашего множества. Они друг друга повторяют один в один. Однако, там упоминается, что в вашем множестве чисел (сравнимых с 1 по модулю 4) разложение на простые множители не однозначно:

$$441\;=\;21\;\cdot\;21\;=\;9\;\cdot\;49$$