Дифференциальные операторы (я чайник)

[Alexzord]

Пытаюсь разобраться с доказательством одного утверждения в книжке. Там определяются такие операторы:

$$A = g(d/dx) (1/g) \quad \quad A^* = 1/g(d/dx) g$$

где $g(x) \in L^2[0,1]$ --- решение уравнения $-y''+q(x)y = \mu y$.

1. Утверждается, что $A^*$ является "формально сопряженным" к $A$ при действительных $g$ и $\mu$. Что это значит?

2. Утверждается, что, используя диф. ур. для $g$ можно получить, что $A^*A = - \frac{d^2}{dx^2} + q - \mu$. Это тоже не понятно, как получить. Изначально даже не совсем понятно, как действуют операторы $A$ и $A^*$. Хотя ниже в книге написано, что

$$Af = g \frac{d}{dx} \frac{f}{g} = f' - f \frac{g'}{g}$$

то есть дифференцируется не $1/g$, а $f/g$.

Прикрепил страничку из книжки на всякий случай:
https://c.radikal.ru/c40/2002/9f/c436b1395186.jpg

[Munin]

Такое впечатление, что вы рано схватились за эту книжку: вам не хватает подготовки, чтобы её читать. То есть, вам нужно сначала освоить матанализ и линейную алгебру за 1 курс, а книжка - примерно для 2-3 курса. Может быть, опирающаяся уже даже на функциональный анализ (2 курс самое раннее).

[Alexzord]

Munin в сообщении #1441190 писал(а):

Такое впечатление, что вы рано схватились за эту книжку: вам не хватает подготовки, чтобы её читать. То есть, вам нужно сначала освоить матанализ и линейную алгебру за 1 курс, а книжка - примерно для 2-3 курса. Может быть, опирающаяся уже даже на функциональный анализ (2 курс самое раннее).

На самом деле я на 4 курсе и книжка примерно на 3-4 курс, потому что там и тфкп, и производные Фреше всякие. Мне бы хотелось некоторые базовые вещи все же понять. Подготовки если не хватает, то не так сильно, как может показаться)

[demolishka]

Alexzord, в формуле для $A$ написана композиция трёх операторов: умножения на функцию $1/g$, дифференцирования по $x$ и умножения на функцию $g$. Функция $g$ фиксирована, а $f$ как переменная. Стало понятней?

[Munin]

Alexzord в сообщении #1441192 писал(а):

На самом деле я на 4 курсе

Ну тогда вы должны были за предыдущие 4 курса хотя бы привыкнуть, как записываются подобные операторы. Это должно было быть и в ОДУ, ДУЧП, и в функане.

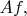
Выражение $A=g\,\dfrac{d}{\,dx\,}\,\dfrac{1}{\,g\,}$ вовсе не означает, что здесь от чего-то надо брать производную. "На пальцах" смысл этого выражения такой: сначала надо записать выражение типа $Af,$ то есть, подействовать оператором на какой-то вектор (здесь - функцию). А потом уже, когда получится в итоге выражение

$$Af=g\,\dfrac{d}{\,dx\,}\,\dfrac{1}{\,g\,}\,\,f,$$

то вот тогда уже вычислять его всё вместе, подразумевая расстановку скобок такую:

$$Af=g\,\Bigl(\dfrac{d}{\,dx\,}\,\Bigl(\dfrac{1}{\,g\,}\,\Bigl(f\Bigr)\Bigr)\Bigr)$$

(то есть, право-ассоциативную). Такой "рецепт" позволит отслеживать выкладки.

А формально смысл этого выражения такой, как указал demolishka.

-- 24.02.2020 13:34:59 --

Понятие "сопряжённый оператор" надо вспоминать из линала и функана. Операторы сопряжены, если для любых двух векторов $(x,Ay)=(A^*x,y).$ А теперь надо расписать эти скалярные произведения как соответствующие интегралы в соответствующем пространстве функций.

-- 24.02.2020 13:38:54 --

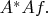
Чтобы найти произведение операторов, например, $A^* A,$ потребуется как-то "применить" один оператор к другому. Делается это так ("на пальцах" опять же): вы записываете выражение, чтобы это произведение подействовало на какую-то произвольную функцию, $A^* Af.$ Потом вычисляете его, по принципу, который я назвал выше, понимая производные в обычном смысле. А потом то, что получилось, надо интерпретировать как действие на эту функцию какого-то одного оператора, $Bf.$ То есть, сумму понимать как сумму; произведение $f$ на какую-то функцию - как оператор умножения на функцию; производную $f'$ - как $\dfrac{d}{\,dx\,}\,f.$

-- 24.02.2020 13:39:46 --

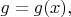
Не забывая, что $g=g(x),$ конечно же.

[Alexzord]

demolishka, да, понятнее. Я не "видел" композицию и оператор умножения на функцию и не понимал, как читать эту запись. Пытался прилепить функцию $f$ справа и не понимал, как это правильнее сделать.
Munin, Насчет сопряженных, я подумал, что может можно без вычисления интегралов как-то лихо получить сопряженный.

Попробую посчитать все эти $AA^*$ и $A^*A$, если упорно не будет сходиться, задам более конкретный вопрос.

(Оффтоп)

В ОДУ, УЧП, функане не встречалась такая запись. Либо встречалась один-два раза и я забыл

[pogulyat_vyshel]

мне как-то немного лениво вчитываться в формулы, но обычно что бы перекидывать производные в интеграле нужны гран условия иначе будут появляться внеинтегральные члены. Ну и еще: если уж давать определение сопряженного оператора то делать это надо как полагается

[Mikhail_K]

pogulyat_vyshel в сообщении #1441222 писал(а):

но обычно что бы перекидывать производные в интеграле нужны гран условия иначе будут появляться внеинтегральные члены. Ну и еще: если уж давать определение сопряженного оператора то делать это надо как полагается

Поэтому и сказано: не "сопряжённый", а "формально сопряжённый" оператор. Это и значит, что всякие возможные неприятности вроде внеинтегральных членов просто игнорируются.

[pogulyat_vyshel]

Mikhail_K в сообщении #1441227 писал(а):

Поэтому и сказано: не "сопряжённый", а "формально сопряжённый" оператор. Это и значит, что всякие возможные неприятности вроде внеинтегральных членов просто игнорируются.

неадекватные определения тоже можно давать на этом основании?

[Alexzord]

pogulyat_vyshel в сообщении #1441222 писал(а):

обычно что бы перекидывать производные в интеграле нужны гран условия иначе будут появляться внеинтегральные члены

Надо сказать, что всё это дело рассказывается в книжке в контексте задачи Дирихле. Хотя в самой лемме, док-во которой я и пытаюсь разобрать, сказано только, что $g$ - решение уравнения $-y''+q(x)y=\mu y$ без всяких граничных условий. Но, видимо, сама по себе сопряженность там не используется. Не разбирался еще до конца. Вот, если интересно, полностью лемма эта.

https://d.radikal.ru/d30/2002/1d/777bcc1c299a.jpg
https://a.radikal.ru/a28/2002/57/629c4103ba7b.jpg
https://a.radikal.ru/a34/2002/db/66c9aefb7417.jpg

[Munin]

Alexzord в сообщении #1441242 писал(а):

сказано только, что $g$ - решение уравнения $-y''+q(x)y=\mu y$ без всяких граничных условий.

Такого не бывает. (Видимо, книжка не очень уж строгая / очень уж нестрогая.)

Даже если у вас нет границ и ограниченной области решения, должны быть наложены граничные условия на бесконечности.

[Утундрий]

Munin в сообщении #1441338 писал(а):

Такого не бывает

Ну, приехали...

[Alexzord]

Munin в сообщении #1441338 писал(а):

Alexzord в сообщении #1441242 писал(а):

сказано только, что $g$ - решение уравнения $-y''+q(x)y=\mu y$ без всяких граничных условий.

Такого не бывает. (Видимо, книжка не очень уж строгая / очень уж нестрогая.)

Даже если у вас нет границ и ограниченной области решения, должны быть наложены граничные условия на бесконечности.

Хм... Ну я полагаю, что там подразумевается, что решение определено на $[0,1]$, почему-то конкретно тут это не указано явно, но ранее в книге уравнение рассматривалось только на $[0,1]$.