Соседние дроби

[melnikoff]

Пусть $a, b, c, d \in \mathbb{N}$.
Назовем дроби $\frac{a}{b}$ и $\frac{c}{d}$ соседними, если $ad-bc=\pm 1$.
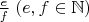
Нужно доказать, что никакая дробь $\frac{e}{f} \;(e, f \in \mathbb{N})$, у которой $f < b + d$, не находится между $\frac{a}{b}$ и $\frac{c}{d}$.
Нужен пинок в правильном направлении.
Пока удалось доказать, что дробь $\frac{a+c}{b+d}$ лежит между $\frac{a}{b}$ и $\frac{c}{d}$ и является соседней по отношению к каждой из них.
Рассмотрим дробь $\frac{a+c}{b+d-k}$, где $k = 1, 2, ..., b+d-1$.
Предположим противное: $\frac{a}{b}<\frac{a+c}{b+d}<\frac{a+c}{b+d-k}<\frac{c}{d}$.
Тогда $\frac{c}{d}-\frac{a+c}{b+d}=\frac{1}{(b+d)d}$ (1) и
$\frac{a+c}{b+d-k}-\frac{a+c}{b+d}=\frac{k(a+c)}{(b+d-k)(b+d)}$ (2).
Ну, я вижу, что для каждого случая расположения 1 в тройном неравенстве можно как-то доказать, что (2) > (1). И всё это доказывает очень мало, ведь $e$ может быть разным... Я уверен, что это ложный путь доказательства. Точно существует какое-то короткое доказательство, так как на него в школе дали не более 10 минут (не в моей школе).

[nnosipov]

melnikoff
Здесь действительно 10 минут хватает, если пойти в правильном направлении. Неравенство $a/b<e/f$ означает, что $af+x=be$ для некоторого натурального $x$. Аналогично можно интерпретировать неравенство $e/f<c/d$ (сделайте это). Далее нужно воспользоваться соотношением $bc-ad=1$. И в итоге будет ясно, почему $f \geqslant b+d$.

[melnikoff]

Не понятно.
Имеем:
$be-af=x$
$cf-ed=y$
$bc-ad=1$.
Как отсюда следует $f \geqslant b+d$ ?
Понял, $f=by+xd \geqslant b+d$.
Спасибо за подсказку.