2. Есть ли какое-то название у этого выражения для исправленной величины, и куда можно на него сослаться?
Ещё раз спасибо!

-- оптимальный линейный прогноз (optimal linear predictor, best linear predictor). Когда его используют, говорят, что применяется модель линейной регрессии (насчёт терминологии я не очень уверен и куда сослаться, не знаю).
1. Получается, что pcov работает только для линейной зависимости от

? Просто в физической литературе эта конструкция представляется как панацея от всего возможного.

и

могут быть 1) условно независимы относительно

, 2) иметь нулевую условную корреляцию относительно

, 3) иметь нулевую частичную корреляцию относительно

. Отношения между этими условиями такие: 1 влечёт 2, а остальные 5 импликаций могут быть неверны (в частности, может быть даже, что

и

условно независимы относительно

, а их частичная корреляция всё-таки ненулевая). Проблема с частичной корреляцией в том, что она рассчитывается через оптимальный
линейный прогноз -- но никто не гарантирует, что линейный прогноз будет хорошим, на самом деле он может быть плохим. Однако ж в некоторых случаях он обязательно хороший; например, если откуда-то известно, что совместное распределение
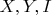
нормально, то 1, 2 и 3 равносильны.
С условной корреляцией такой проблемы нет, потому что она считается через настоящий (необязательно линейный) оптимальный прогноз (то есть условное математическое ожидание). Но считать её сложнее.