ilghizОбщее впечатление от задачи: безнадёга...
Вот некоторые соображения.
1. Про интегральное уравнение-1
1.1. Дифференцирование.
Если уравнение допускает дифференцирование по игрек, то имеем: надо найти эф, ортогональную (в Эль-2 на минус-эль-эль) всем производным от "у" (и не ортогональную самой "у"). Частные случаи:
1.1.1.

- многочлен (степени 3, например). Частное решение - ортогонализируем систему

, в качестве

берем четвертый вектор (с множителем); всего решений - до фига (общее решение получаем из частного, добавляя к нему произвольную функцию, ортогональную подпространству многочленов степени не выше 3).
1.1.2.

- квазимногочлен (т.е., комбинация экспонент с коэффициентами-многочленами). Такое

есть решение линейного однородного диф. ур-я с постоянными к-тами. Его производные порождают конечномерное подпространство. Если само

есть линейная комбинация его производных - то решений нет! (Простейший пример такого типа уже указал ранее
mihiv).
1.1.
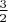
. Гибрид двух предыдущих - дает разрешимость, с большим кол-вом решений.
1.1.3. Общий случай. Аппроксимируем заданную

многочленами, и запустим процедуру из п. 1.1.1. Надежда получить решение - совершенно иллюзорна, хотя бы из-за примеров 1.1.2.
1.2. Основной путь - ряды Фурье. Разлагая

в ряд Фурье на
![$[-2L,2L] $ $[-2L,2L] $](https://dxdy-01.korotkov.co.uk/f/0/1/d/01da72bf98fa1a0a8dff8260f35f8f2882.png)
(а

- на
![$[-L,L]$ $[-L,L]$](https://dxdy-02.korotkov.co.uk/f/9/2/f/92f4fcd1379869ce7cbee0ab2d487f4682.png)
), и перераскладывая "неправильные" (с нечетными номерами) экспоненты, получим (бесконечную) систему линейных уравнений на к-ты

(с "теплициевой" матрицей. Видимо, ТС так и делал). Разрешимость полученной системы крайне сомнительна (а "обрезание" ее, решение "обрезанной" и надежда на сходимость - тож) - см. ниже.
1.3. Вообще-то, мы имеем дело с классическим интегральным уравнением первого рода (разве что только ядро вполне себе специфично). Что мы знаем: соответствующий интегральный операрор - компактен.
Если он - конечномерный - попадаем в п. 1.1.1-1.1.2.
Но вот если - нет -- караул... За исключением специально подобранных случаев, (а конкретные функции ТС на такое как-то не тянут) решение не получить. Задача, как мы знаем, некорректна; поэтому всякие аппроксимации, как правило, ничего не дают: нет сходимости.
2. Уравнение-2. Как я понимаю, сдвигами аргумента эту задачу можно свести к задаче-1 (рассматривая функцию

, равную

на одном участке оси, и равную (сдвинутой)

на другом, с соответствующим надругательством над

). Поэтому выводы про задачу-1 остаются справедливыми и для задачи-2



