Спасибо за идею. Она, однако, требует некоторого уточнения. Во-первых, выбранные Вами множества
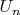
не обязаны быть компактными - простейший контрпример:
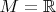
,

,

. Тем не менее, исчерпание множества

компактными подмножествами существует (существует для любого локально-компактного и хаусдорфова топологического пространства со счётной базой - например, J. Lee "Introduction to Smooth Manifolds", second ed., 2012, A.60). Во-вторых, приведённое рассуждение непосредственно применимо, видимо, только лишь к подмножествам

. В-третьих, я, к сожалению, не знаком с использованными Вами обозначениями для нормы на пространстве функций - могу лишь предположить, учитывая Ваши дальнейшие пояснения, что она вычисляется на основе значений самой функции и

первых её производных.
Пусть

- открытое подмножество,

- исчерпание

компактными подмножествами,

,
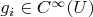
,

- набор функций,
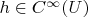
- произвольная функция. Множества

замкнуты в

, как компактные подмножества хаусдорфова пространства. Поэтому мы можем определить гладкие на

функции

и

:


Пусть


Определим функции

и

как формальные ряды функций:

Эти ряды равномерно сходятся как для самих функций, так и для их формальных производных, поэтому

и

- гладкие на

. Функция

положительно определена на

, поскольку для любой точки

всегда найдётся

такое, что

, а значит


. Функция же

удовлетворяет условию:

. Требуемые функции найдены.
Теперь, пусть

- произвольное гладкое многообразие,

- гладкий атлас,

наследует гладкую структуру из

. Функция
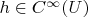
задаёт гладкую функцию

на каждом открытом в

подмножестве

, если

. Как уже было показано, для этой функции существуют гладкие на всём

функции

и

такие, что

продолжается до

. Ограничивая эти функции на множество

, получаем, что существуют функции
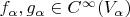
,

,

, для которых справедливо утверждение, что

продолжается до

. Пусть

- разбиение единицы, подчинённое покрытию

. Тогда функции
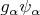
и
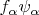
продолжаются до функций, гладких на

. Построим

и

, где суммирование идёт по всем значениям

, для которых выполняется условие

. Эти функции также гладкие на

, и

(так как все

) и

. Утверждение доказано.
P.S. Вместо исчерпания компактными подмножествами мы могли бы взять счётное покрытие

предкомпактными в нём открытыми шарами, а вместо выбранных

функции, которые положительно определены каждая на своём шаре из покрытия и равные нулю вне его. Дальнейшие рассуждения остались бы справедливы.