Допустим, среднестатистический человек способен определять массу предмета у него в руках с погрешностью

, подчиняющейся нормальному распределению с матожиданием

и стандартным отклонением

.
Можно ли интерпретировать плотность распределения погрешности

как функцию, характеризующую вероятность того, что масса предмета с точностью до заданного числа знаков после запятой отличается на заданную величину от оценки массы предмета?
Например, при
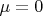
,

и точности до

имеем: с

масса предмета равна её оценке, с

масса предмета на единицу больше или меньше оценки и т.д.
Иными словами, масса предмета с достоверностью

равна оценке массы, масса предмета с достоверностью

равна (оценка массы

) или (оценка массы

) и т.д.
Ещё вопросы:
1) Верны ли мои рассуждения?
2) Можно ли интерпретировать плотность вероятности случайной величины как «плотность достоверности» неслучайной величины?
3) Как математики называют распределения, описывающие достоверность событий?
4) Можно ли понимать достоверность как вероятность того, что неслучайная величина равна заданному значению?



