Если ТС ничего не путал, то
очевидно следует использовать очень сильное утверждение
(я бы только сказал, что ноль туда не вписывается, но если заменить единицей, то да; теги
oeis для удобства в цитате добавил).
Если у нас есть рекуррентные формулы для той и этой, то простым способом получится и формула для последовательности, полученной их перемежением: если

,

, где

— какие-то выражения, поминающие соответственно

и

от каких-то связанных с

аргументов, и
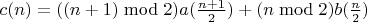
, то

. Основную проблему представляет найти выражения

.
(Или ТС неправ и его последовательность может оказаться проще. Вообще подозрительное конечно описание, если вот честно.)
-- Пн янв 20, 2020 03:51:59 --Хотя иногда зависимость от

напрямую в рекуррентной формуле не допускают. Ну тогда всё просто ещё хуже.



