Не понимаю одного момента в доказательстве счётности алгебраических из книги Виленкина "Рассказы о множествах" (страницы 69-70):
Цитата:
..отметим сначала, что каждое число рассматриваемого вида является корнем алгебраического уравнения вида

, (1)
где

и

— целые числа. Например,

корень уравнения

,
![$\sqrt[3]{5}$ $\sqrt[3]{5}$](https://dxdy-03.korotkov.co.uk/f/a/3/c/a3c02a4641df0d460878a3cf197de12282.png)
корень уравнения

.
Сначала перенумеруем все целые числа (нулю и натуральным числам присвоим нечётные номера, а отрицательным — чётные).
Номер целого числа

обозначим
через

[такая же буква в формуле, только жирная]. Каждому уравнению вида (1) поставим в соответствие число

[степени жирненькие]
(через

здесь обозначено
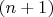
-е простое число). Например,
уравнению

ставим в соответствие номер

(потому что целое число

имеет номер 4,

— номер 1, а целое число

— номер 7). Теперь каждое уравнение получило свой номер,
причем разным уравнениям соответствуют разные номера (каждый
номер N единственным образом разлагается на простые множители,
то есть единственным образом задает числа
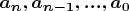
; этим же
числам соответствуют определенные целые числа

,
а тем самым и определенное уравнение

)
Тогда какому уравнению соответствует N=1? Мне кажется, что никакому; может, я что-то не так понял? Автор и до этого сформулировал основную теорему арифметики соответствующим образом:
Цитата:
Читатель,конечно, помнит, что любое натуральное число единственным образом разлагается на простые множители.
не уточняя, что натуральное число должно быть больше единицы. Подскажите, пожалуйста.
UPD: Только что дошло, что

может ничего не соответствовать, так как нумерация нужна, чтобы выписать корни, которые впоследствии будут пронумерованы, начиная с единицы.