Полный порядок в иррациональных числах

[CMTV]

Пытаюсь построить множество действительных чисел через расширение $\mathbb{Q}$ с помощью сечений.

Иррациональное число в таком подходе — сечение $A|A'$ на множестве $\mathbb{Q}$, где у нижнего класса $A$ нет наибольшего элемента, а у верхнего класса $A'$ нет наименьшего. Другими словами, иррациональным числами мы называем щели в $\mathbb{Q}$.

Далее вводим отношения "равенства" и "больше" для любых двух иррациональных чисел $\alpha = A|A'$ и $\beta = B|B'$:

$$ \alpha = \beta :\Leftrightarrow (A=B) \land (A' = B') \qquad \quad \alpha > \beta :\Leftrightarrow B\subset A $$

Легко показать, что для равенства достаточно равенства или верхних классов, или нижних. Так же легко показать, что $\alpha > \beta \Leftrightarrow A' \subset B'$.

Теперь нужно доказать, что множество иррациональных чисел является линейно упорядоченным, то есть

$$ \boxed{\forall \alpha, \beta \in \mathbb{I} : \ (\alpha = \beta) \lor (\alpha > \beta) \lor (\beta > \alpha)} $$

Собственно, доказать это у меня и не получается. Ниже привожу мой вариант доказательства, которое я почти довел до конца, но застрял в самом конце.

Хотел попросить помощи в доказательстве. Еще лучше будет, если существует какое-то простое доказательство, а то с этим я уже настрадался.

--- Доказательство ---

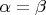
Пусть нам даны два произвольных иррациональных числа $\alpha = A|A'$ и $\beta = B|B'$. Если $\alpha = \beta$, то все в порядке. В противном случае $\alpha \neq \beta$.

$$ \alpha \neq \beta \Leftrightarrow (A\neq B) \lor (B'\neq A') $$

Так как в выражении стоит логическое ИЛИ, имеем 3 возможных варианта:
1. $(A=B)$ и $(A'\neq B')$
2. $(A\neq B)$ и $(A' = B')$
3. $(A\neq B)$ и $(A' \neq B')$

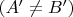
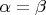
Первые два варианта сразу ведут к тому, что $\alpha = \beta$. Значит, только третий вариант годится для неравных друг другу $\alpha$ и $\beta$.

$$ \alpha \neq \beta \Leftrightarrow (A\neq B)\land (B'\neq A') $$

В этом выражении можно заменить $A\neq B$ и $B'\neq A'$ на результат вот такой леммы, которая справедлива для любых множеств $A$ и $B$:

$$ A\neq B \Leftrightarrow (B\nsubseteq A)\lor (B\subset A) $$

(ее можно достаточно быстро доказать от противного)

$$ \alpha \neq \beta \Leftrightarrow \big[ (B\subset A) \lor (B\nsubseteq A) \big] \land \big[ (A'\subset B') \lor (A'\nsubseteq B') \big] $$

Разобьем это выражение на 4 скобки:
\begin{gather*} \alpha \neq \beta \Leftrightarrow \\ \Leftrightarrow \big[\overbrace{ (B\subset A) \land (A' \subset B') }^{\alpha > \beta}\big] \lor \big[\overbrace{(B\subset A)\land(A'\nsubseteq B')}^{0}\big] \lor \big[\overbrace{(B\nsubseteq A)\land (A'\subset B')}^{0}\big]\lor \\ \lor \big[\overbrace{(B\nsubseteq A) \land (A'\nsubseteq B')}^{\text{?}}\big] \end{gather*}

В первой квадратной скобке обе под-скобки обозначают одно и то же: $\alpha > \beta$.

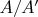
Вторая скобка всегда ложна, так как $A'\nsubseteq B'$ означает существование такого $a' \in A'$, который не лежит в $B'$. Значит, $a'\in B$ (по определению сечения). В левой части скобки имеем $B\subset A$, а значит $a' \in A$. Итак, $a' \in A$ и $a' \in A'$, а это противоречит определению сечения $A/A'$, которое задает число $\alpha$.

Третья скобка всегда ложна по той же причине.

Запишем еще раз большое высказывание выше, на этот раз заменяя скобки найденными значениями:

$$ \alpha \neq \beta \Leftrightarrow (\alpha > \beta) \lor 0 \lor 0 \lor \big[ (B\nsubseteq A) \land (A'\nsubseteq B') \big] $$

$$ \alpha \neq \beta \Leftrightarrow (\alpha > \beta) \lor \big[ (B\nsubseteq A) \land (A'\nsubseteq B') \big] $$

Итак, осталось только показать, что правая квадратная скобка является как раз $\beta > \alpha$, то есть

$$ \big[(B\nsubseteq A) \land (A'\nsubseteq B')\big] \Leftrightarrow \big[(A\subset B)\land(B'\subset A')\big] \Leftrightarrow \beta > \alpha $$

У меня почти получилось это сделать. По определению, $A\subset B$

$$ A\subset B \Leftrightarrow (A\subseteq B) \land (A\neq B) $$

Но $A\neq B$ и так истинно, поэтому его можно опустить.

$$ A\subset B \Leftrightarrow A\subseteq B $$

Нужно лишь показать, что в контексте нашей задачи с сечениями

$$ A\subseteq B \Leftrightarrow B\nsubseteq A $$

Докажем $\Rightarrow$ от противного:

$$ (A\subseteq B) \land (B\subseteq A) \Leftrightarrow (A=B) $$

Получили противоречие, так как $A\neq B$. Докажем теперь $\Leftarrow$ тоже от противного:

$$ (B\nsubseteq A)\land (A\nsubseteq B) $$

Это вроде как "очевидно". Другими словами, и так понятно, что либо нижний класс $\alpha$ целиком лежит в нижнем классе $\beta$, либо нижний класс $\beta$ целиком лежит в нижнем классе $\alpha$. Не может быть так, что они лишь частично пересекаются (или не пересекаются вовсе). Но строго доказать наличие противоречия тут у меня так и не получилось. А ведь это последний элемент мозаики...

[CMTV]

Кажется, понял. Напомню, что я пытаюсь доказать ложность $(B\nsubseteq A) \land (A\nsubseteq B)$.

Из левой скобки получаем, что существует рациональное число $b\in B$, но не принадлежащее $A$. Тогда $b\in A'$ (по определению сечения). Из правой скобки получаем таким же путем получаем, что есть некоторое рациональное число $a\in A$, которое принадлежит уже $B'$.

Итак,

$$ a\in A \qquad a\in B' \qquad b\in B \qquad b\in A' $$

Но, по определению сечения, $a$, лежащее в $B'$ должно быть больше $b$, лежащее в $B$:

$$ a > b $$

С другой стороны, $b$, лежащее в $A'$ должно быть больше $a$, которое лежит в $A$:

$$ b > a $$

Итак, получаем противоречащие друг другу выражения (так как множество рациональных чисел линейно упорядочено):

$$ (a>b) \land (b>a) $$

Итак, доказана правильность следующего высказывания для сечений и при условии, что $A\neq B$:

$$ A\subset B \Leftrightarrow A\subseteq B \Leftrightarrow B\nsubseteq A $$

Возвращаемся к доказываемому выражению:

$$ \alpha \neq \beta \Leftrightarrow (\alpha > \beta) \lor \big[ (B\nsubseteq A) \land (A'\nsubseteq B') \big] $$

Пользуясь доказанной эквивалентностью можно спокойно заменить $B\nsubseteq A$ на $A\subset B$, а $A'\nsubseteq B'$ на $B'\subset A'$.

$$ \alpha \neq \beta \Leftrightarrow (\alpha > \beta) \lor \big[ (A\subset B) \land (B'\subset A') \big] $$

Правая скобка теперь не что иное, как повторенное дважды определение $\beta > \alpha$:

$$ \alpha \neq \beta \Leftrightarrow (\alpha > \beta) \lor (\beta > \alpha) $$

Осталось лишь исключить случай, когда $\alpha > \beta$ и одновременно $\beta > \alpha$. Но в этом случае получаем, что $(A\subset B)\land (B\subset A)$, а это сразу приводит к противоречию, значит

$$ \alpha \neq \beta \Leftrightarrow (\alpha > \beta) \dot{\lor} (\beta > \alpha) $$

Итак, окончательно доказано, что

$$ \forall \alpha,\beta \in \mathbb{I}: \ (\alpha = \beta) \lor \Big( (\alpha > \beta) \dot{\lor} (\beta > \alpha) \Big) $$

$\blacksquare$

Если что, я все еще не откажусь от какого-нибудь более простого способа
Кажется, теперь мне понятно, почему Фихтенгольц решил апеллировать к геометрической наглядности вместо строго доказательства

[mihaild]

С учетом ваших первых нескольких строчек достаточно следить только за нижним классом (и сечения часто ровно так и определяются).
Неравенство множеств $A \neq B$ сразу записываем как существование элемента, принадлежащего одному множеству, но не другому: $\exists x \in \mathbb Q: (x \in A \wedge X \notin B) \vee (x \notin A \wedge x \in B)$.
Не ограничивая общности, рассмотрим первый случай (второй аналогично): $x \in A \wedge x \notin B$. Но раз $B$ - нижний класс, то, если $y \in B$, то $y < x$. А раз $A$ - нижний класс, то, если $y < x$ то $y \in A$. Т.е. если $y \in B$ то $y \in A$, откуда $B \subseteq A$.

Это конечно менее строго, чем у вас, и при расписывании разрастется еще раза в 3 по объему, но кажется всё равно проще получается.

CMTV в сообщении #1435607 писал(а):

$$ \alpha \neq \beta \Leftrightarrow \big[ (B\subset A) \lor (B\nsubseteq A) \big] \land \big[ (A'\subset B') \lor (A'\nsubseteq B') \big] $$

Вот здесь достаточно оставить в правой части только одну скобку, и дальнейшие рассуждения сразу становятся короче (а с учетом того что нам тут не нужна эквивалентность, достаточно следствия, это сделать совсем просто).