Без картинок сложно воспринимать, но рисовать не в чем сейчас, поэтому максимально описательно в конце...
Разумеется, если в множествах есть общие элементы, то ответ очевиден. Поэтому считаем, что

Немного очевидной арифметики.
Пусть мы подобрали такое множество

. Очевидно, его дополнение до
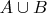
тоже удовлетворяет всем условиям.
Введем обозначения:


По построению,

Обозначая малыми буквами соответственные суммы множеств, получим следующие соотношения:

где

Следовательно,

Иными словами, утверждение задачи эквивалентно следующему: найдутся такие подмножества множеств

и

(непустые, и их дополнения непустые), что их суммы отличаются не более, чем на 1/2.
Упорядочим оба исходных множества и рассмотрим последовательности их кумулятивных сумм - начинаются они, разумеется, с наименьшего элемента (который не более 1), а заканчиваются числом

. Если в этих последовательностях найдутся два члена, отличающиеся друг от друга менее чем на 1/2, "обменный блок" найден.
Также можно заметить, что предпоследние члены в обеих последовательностях не меньше 1/2, но не больше

(максимальный элемент множества по определению не меньше 1, но не больше

).
Помеcтим на числовой оси точки с этими подсуммами на интервале от 0 до

- для множества

сверху, для

- снизу. Далее считаем, что точки не совпадают. Длины отрезков, понятно, соответствуют числам множества.
Рассмотрим пока для множества

. Внутри интервала

расставлена

точка. Самая левая из них может находиться где угодно на полуинтервале

, а вот самая правая - не правее от

.
Итак, на числовую ось уложены отрезки неубывающей слева направо длины, всего их

, и суммарная длина не превышает

. Следовательно, существует точка

, слева от которой лежат отрезки длины не больше 1.
Предположим, что она не крайняя слева, и для

тоже (если нет - переназовем множества и см. дальше).
У нас два множества, поэтому и точки тоже две. Выберем левую. Без ограничения общностей считаем, что она разделяет два отрезка, полученные из множества

. Кроме того, она лежит на одном из отрезков, относящихся к

, и длина этого отрезка менее единицы, поэтому расстояние до одного из его концов менее 1/2.
Если же

- крайняя слева, это значит, что наименьший элемент

меньше единицы, а остальные - больше, но тогда, по построению, все они находятся на интервале

, и числовая ось справа от

разбита на отрезки длины
чуть больше единицы, всего их

.
Если это выполняется и для

, то мы просто обмениваем два наибольших элемента (например) - разница не превышает

, что нам и нужно. Исключение - случай двойки, но он тривиален, разбирается "вручную".
Пусть для

не выполняется: точка

не крайняя левая. Тогда, чтобы условие в задаче не выполнялось, все точки этой последовательности должны находиться:
- посередине между каждого отрезка (для

, кроме правого
- левее от

.
Если точек первого типа нет, то одно из чисел должно быть больше

, что противоречит условию.
Если есть хотя бы две точки первого типа, то видно, что в

есть число, близкое (с точностью

) к целому, и мы обмениваем его с необходимым набором "почти единиц".
Если ровно одна точка первого типа, это значит, что сумма всех элементов

, кроме двух наибольших, равна

, наибольшее число - "почти полуцелое", тогда дробная часть промежуточного числа отличается от целого на величину не более

- то есть ближе к целому, чем 1/2. Это значит, что, подобрав нужное количество "почти единиц", мы найдем "обменную часть" из
