Вы бы определились, являются ли у вас массивы
xd,
yd и
zd одномерными или двумерными. А то вы меняете это как попало, в итоге скрипт просто падает с ошибкой и до рисования графиков дело не доходит.
-- 02.12.2019, 21:55 --А, да, удалять данные перед построением по ним графика - это тоже очень, очень хорошая идея.
 -- 02.12.2019, 21:57 --
-- 02.12.2019, 21:57 --Собрался писать про третью ошибку, после чего подумал, что надо остановиться. Удалите этот ужас и сделайте все заново. Настоятельно рекомендую писать комментарии к коду с пояснениями, что именно вы надеялись сделать в каждой строке.
Да, вы правы. Я этот код писал на основании кода, найденного в интернете. Он был для более простой функции, но график строился нормально. И перед построением данных стирались первые

значений переменной. Так и не смог понять, почему именно так.
Написал свой код:
%Бифуркационная диаграмма для аттрактора Ресслера
%для p
%Задаем параметры
N = 100; %количество итераций по переменным x, y, z
a = 0.2;
c = 5.7;
dt = 0.01;
alpha = 6;
pstep = 0.01; %шаг по переменной p
pmax = 10; %максимальное значение переменной p
Np = 1000; %количество итераций по переменной p
% задание пустых массивов
xd = [];
yd = [];
zd = [];
p = [];
% задание начальных условий для переменных
p(1:N,1)=0;
xd(1,1:Np) = 5;
yd(1,1:Np) = 10;
zd(1,1:Np) = 20;
for j = 2:1000
for i = 2:N
xd(i,j-1) = xd(i-1,j-1)-dt*(alpha*(yd(i-1,j-1)+zd(i-1,j-1)));
yd(i,j-1) = yd(i-1,j-1)+dt*(alpha*(xd(i-1,j-1)+a*yd(i-1,j-1)));
zd(i,j-1) = zd(i-1,j-1)+dt*(alpha*(p(i-1,j-1)+zd(i-1,j-1)*(xd(i-1,j-1)-c)));
end
p(:,j) = p(:,j-1)+pstep; % изменение переменной p на величину шага по этой переменной
end
plot(p,xd,'k.','MarkerSize',3); %построение графика
xlabel('p'); ylabel('x'); %подпись осей
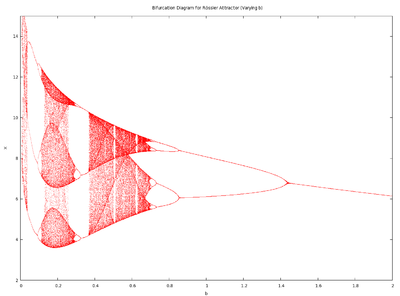
График строится, но он сильно отличается от той бифуркационной диаграммы, которая приведена для параметра

аттрактора Рёсслера в Википедии.
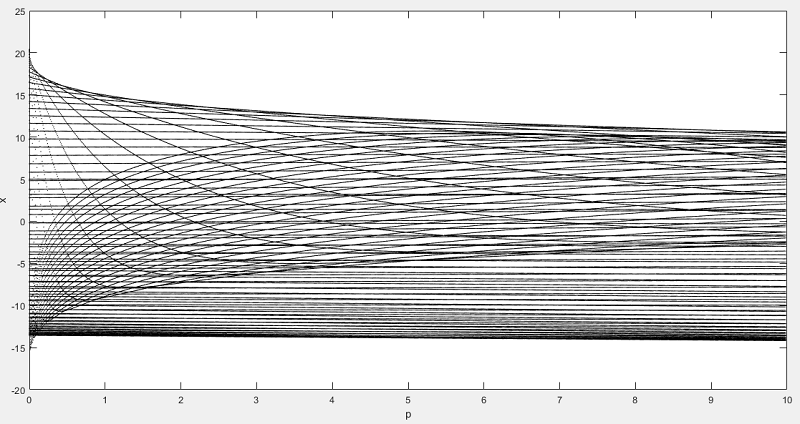
То, что получилось у меня:
То, что должно получиться в теории: