Попытался привести пример такой нелинейной функции и вышло, вроде, что-то похожее на правду.
Положим

для всех

, тогда условие (1) задачи переходит в

для всех действительных

, а условие (2) равносильно
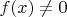
при

. Пусть

- множество действительных чисел
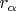
таких, что всякое действительное число

является единственной линейной комбинацией конечного числа элементов из

с рациональными коэффициентами

Обозначим через

множество, являющееся объдинением множества всех рациональных чисел, алгебраических чисел и трансцендентных чисел, степень трансцендентности которых не превосходит

. Очевидно, что тогда любая конечная линейная комбинация элементов

с рациональными коэффициентами принадлежит

. Пусть

есть подмножество

, обладающее свойством, аналогичным множеству

: т.е. является "базисом" в

.
Множества

и

имеют мощность континуум. Пусть

- биекция. Доопределим функцию

для всех действительных

следующим образом: если

имеет вид

, то

при этом

.
Заданная таким образом функция

удовлетворяет условию (1), т.к.

.
А также условию (2), поскольку

при

противоречило бы определению базиса. В некотрых здесь терминах я не очень разбираюсь, так что, заранее извиняюсь, если что не так.