Комплексные числа в геометрии

[SNet]

В отчаянии пишу сюда и прошу о помощи.

Задача:
Докажите, что в прямоугольном треугольнике с неравными катетами биссектриса прямого угла делит пополам угол между высотой и медианой, проведёнными из той же вершины

Я знаю, как решить эту задачу геометрически, но нужно комплексными числами. Итак, пусть треугольник у нас ABC с острым углом C. Тогда CM -- медиана, CP -- биссектриса, CH -- высота. Ввожу соответствующие комплексные координаты: m, p и h. Тогда нужно доказать, что $\arg(\frac{m}{p} )=\arg(\frac{p}{h})$, т.е. $\arg(\frac{mh}{pp})=0$, т.е. что число $\frac{mh}{pp}$ действительное. Как это сделать я ума не приложу. Подскажите, с чего хотя бы начать.

[Утундрий]

(Оффтоп)

SNet в сообщении #1424392 писал(а):

в прямоугольном треугольнике с нервными катетами

Держитесь от такого треугольника подальше!

[Sicker]

SNet
Я бы расписал ваши $m,p,h$ через катеты $a,b$, и показал равенство нулю множителя при $i$

-- 06.11.2019, 19:32 --

P.S. И забил бы на их длины

[Xmas]

В "плоских" геометрических задачах (в планиметрии, если выражаться культурно), комплексная плоскость получается заменой $y$ на $jy$. Вместо пары координат имеете одну комплексную, $x+jy$. На чертежах всё выглядит точно так же, как в обычных координатах "x-y", и все построения те же, не считая буквы $j$, или $i$ перед подписью "$y$" возле координатной оси. Выбор буквы ($i$ или $j$) зависит от предпочтений преподавателя.

Вам не нужно вводить специальные "комплексные координаты". Был, скажем, классический треугольник со сторонами 3,4,5 (4 - длинный катет вдоль $x$, 3 - короткий катет вдоль $y$). Стал треугольник с комплексными координатами вершин: длинная $a=4+j 0$, короткая $b=0+j 3$.

От комплексных чисел всегда можно вернуться назад: первое слагаемое будет $x$, второе, с отброшенным $j$ - будет координатой $y$. Но в комплексной арифметике появляются дополнительные удобства. Например, умножение комплексной координаты (точки), на $\cos\varphi +j\sin \varphi$, равнозначно её повороту вокруг начала координат на угол $\varphi$. Это можно расписать и раздельно, с помощью косинуса и синуса, но с комплексными числами получается компактнее.

Попробуйте. Если что-то не пойдёт, пишите. Я поставлю подписку на тему. Об ответах нынешние андроиды уведомляют почти сразу.

[SNet]

Xmas
Это всё понятно, но суть в том, чтобы решить задачу исключительно методом комплексных чисел (и смежных с ними векторов)

-- 06.11.2019, 20:06 --

Sicker
Чересчур нехорошие скобки получаются

[Xmas]

SNet, я прям сейчас набираю ответ чисто в комплексном духе. Я сделаю ещё рисуночек, так что прошу малость подождать. Около получаса. У меня уже ночь, так что я в неторопливом состоянии :) Отдыхаю, так сказать.

[SNet]

Xmas
Буду ждать!

[nnosipov]

SNet в сообщении #1424392 писал(а):

В отчаянии пишу сюда и прошу о помощи.

А кто или что заставляет Вас решать эту задачу с помощью комплексных чисел? Ведь Вы ее уже решили геометрически. Комплексные числа Вы не знаете как применить, что уже само по себе странно, ибо к ним обычно прибегают, когда вообще думать не хочется, а хочется просто тупо получить требуемый результат, или задача очень сложная, не поддается геометрическими методами. Комплексные числа --- это ведь очень простая вещь с точки зрения технологии, которая заранее гарантирует успех (можете вот здесь посмотреть: topic75858.html, к сожалению, там сложные примеры). Видимо, Вам просто не объяснили, как она работает алгоритмически, отсюда и затруднения.

Но в данном случае непонятно, стоит ли ради одной колосинки заводить весь этот комбайн. Надеюсь, будет найден какой-то компромисс.

[SNet]

nnosipov
Я стараюсь самостоятельно овладеть вот этой технологией по книге Понарина. Где-то, видимо, действительно дыра, но тогда её надо устранить

(Оффтоп)

Либо я просто глупый

[nnosipov]

SNet в сообщении #1424410 писал(а):

Я стараюсь самостоятельно овладеть вот этой технологией по книге Понарина.

Понятно. Тогда Вы наполовину мой клиент (я имею в виду компьютерно-алгебраический аспект), рекомендую пройти по ссылке выше и почитать не торопясь.

Другое дело, что Понарин еще и геометрией занимается. В общем, Вам придется решать, в какую сторону делать крен.

[SNet]

nnosipov
Сейчас проблемы только с задачами на углы. Но если поможет, то пойду читать

[nnosipov]

SNet
Сейчас у нас уже поздно. Если возникнут вопросы, пишите здесь, постараюсь помочь. Во всяком случае, можно будет продемонстрировать общий подход на этой Вашей конкретной задаче. Это будет упражнение по программированию

[Xmas]

Пусть первый катет идёт вдоль оси $x$, длина $a$. Ему сопоставляется
комплексное число $a+j 0$. Второй катет длиной $b$ вдоль оси $y$. Ему сопоставляется число $0+jb$.

1) Высота треугольника, проведенная из вершины при катетах - это перпендикуляр к гипотенузе. Гипотенуза проходит между вершинами $b,a$. Перпендикуляр к гипотенузе будет перпендикулярен и другим прямым, параллельным гипотенузе. Из них есть одна особенно удобная, которая проходит через точки $(0,0)$ и $(a,-b)$.

Начало координат $(0,0)$ дальше подразумевается молча. Можно говорить, что прямая задаётся (одной!) точкой $p+jq$, надеясь, что все догадаются, что вторая точка имелась в виду $(0,0)$.

Итак, координаты гипотенузы знаем: $(a,-b)$. Перпендикуляр к ней получается поворотом на $90^\circ$, что в комплексных числах равнозначно умножению на $0+j$. Получаем: $ (a-jb)\cdot(0+j) = b+ja$. (это результат (1)).

2) Находим координаты медианы. Это совсем просто. Одна вершина плюс вторая, разделить пополам:
$\frac{a+jb}{2} = \frac{a}{2}+j\frac{b}{2}$. Это результат (2).

3) Искомое доказательство - что биссектриса делит угол между высотой и медианой пополам. То есть, что полусумма аргументов (углов) высоты и медианы равна $45^\circ$.

Проверяем. Тангенс угла медианы $b/a$, тангенс угла высоты $a/b$. Формула сложения арктангенсов - это, например, "Абрамович-Стигун", формула 4.4.34, либо Фихтенгольц 1-й том, внизу 113-й страницы, $\arctg x + \arctg x = \arctg \frac{x+y}{1-xy}$

По этой формуле получается, что аргумент арктангенса суммы - бесконечность, значит, полный угол $90^\circ$. Их биссектриса, значит, всегда $45^\circ$. Ну и биссектриса прямого угла тоже всегда $45^\circ$. Вывод, что одно всегда равно другому, можно завершить по вкусу.

[SNet]

Xmas
Спасибо за поучительное решение! Начинаю разбираться.

[arseniiv]

SNet в сообщении #1424392 писал(а):

с неравными катетами

Кстати ненужная оговорка. Она убирает случай, когда угол между высотой и медианой нулевой, но и углы между высотой и биссектрисой и биссектрисой и медианой тоже по нулям, так что всё ещё делит пополам. Наверняка решение этот случай никак не будет выделять. (Решение Xmas не читал; я бы вписал этот треугольник в единичную окружность или, если единичная кажется слишком единичной, в любую окружность $|z| = R$. В таком случае медиана удобная, высота удобная, биссектриса может показаться сперва не очень удобной, но мне думается, это окупается.)

-- Чт ноя 07, 2019 00:20:30 --

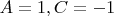
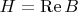
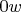
То есть (всё ещё не подсматриваю решение выше) пусть $\triangle ABC$, $B$ — вершина при прямом угле. Тогда берём $A = 1, C = -1$ и $|B| = 1$. Медианой будет $B0$, высотой $BH$, где $H = \operatorname{Re} B$. Теперь нам надо прийти к выражению для биссектрисы угла. Посмотрим сначала на некоторые лучи $0z, 0w, 0v$; чтобы $0w$ был биссектрисой $\angle z0v$, надо, чтобы поворот от одной стороны к биссектрисе был удвоенным поворотом от одной стороны до другой, то есть $(z/w)^2 = kz/v$, где $k\in\mathbb R$. 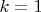Если мы хотим найти хоть какое-нибудь $w$, можем положить $k = 1$ и получим $w^2 = zv$. 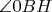Теперь посчитаем биссектрисы $\angle ABC$ и $\angle 0BH$: первая будет идти в направлении $w_1$, вторая $w_2$;

$$w_1^2 = (A - B)(C - B) = (B - 1)(B + 1) = B^2 - 1;$$

$$w_2^2 = (B - 0)(B - H) = B(B - \operatorname{Re} B) = i B\operatorname{Im} B.$$

Ожидаем, что $w^2_1/w^2_2$ будет вещественным:

$$\frac{B^2 - 1}{i B\operatorname{Im} B} = \frac{B - \overline B}{i\operatorname{Im} B} = \frac{2i\operatorname{Im} B}{i\operatorname{Im} B} = 2.$$

(Здесь я наконец-то воспользовался единичным модулем $B$, от которого $B^{-1} = \overline B$.) Ура!

Неучтённая деталь: мы могли получить, что биссектрисы того и того угла перпендикулярны, а не совпадают как прямые. Это надо отдельно проверить.

-- Чт ноя 07, 2019 00:23:06 --

Посмотрел наконец доказательство выше. Не, мне нравится моё. Оно почти не поминает никаких координат. Если бы я не упрощал жизнь и не располагал $A, B, C$ хитрым образом (как и Xmas), то получились бы совсем инвариантные выкладки, но длиннее.

-- Чт ноя 07, 2019 00:26:56 --

Сейчас я вроде понял, что стоило идти другим путём — отразить всё относительно биссектрисы. Это должно было бы перевести каждый из углов в себя, притом мы не получили бы лишнюю возможность перпендикулярности, потому что не возводили бы ничего в квадрат (не поминали бы двойной поворот, который и рождает этот второй случай).

-- Чт ноя 07, 2019 00:28:11 --

SNet
Вот попробуйте с отражением. Отражение относительно вещественной прямой — это просто комплексное сопряжение, а отражение относительно другой можно получить, скомбинировав его с поворотами.

-- Чт ноя 07, 2019 00:31:07 --

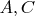
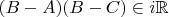
Но тогда удобнее будет уже расположить $B$ в нуле (опять как у Xmas). А вот $A, C$ можно попробовать специально нигде не фиксировать по отдельности, а наложить инвариантное условие на прямоту $\angle ABC$: $(B - A)(B - C)\in i\mathbb R$ (ну, без нуля). Если всё получится, у вас будет самое чистейшее решение в комплексных числах, к которому не придраться.