Вы меня опередили. Я тут немного по-своему разобрался... оно будет ниже.
Оба определения из книги "Лекции по теории графов" авторы: В.А. Емеличев, О.И. Мельников, В.И. Сарванов, Р.И. Тышкевич.
Из второго определения следует, что у неплоских графов нет граней. А вернее --- понятие грани определено только для плоских графов.
А из первого определения следует, что в неплоском графе, уложенном на плоскости, найдется хотя бы одна пара вершин, которые невозможно соединить жордановой кривой, не пересекающей ребра графа.
Хмм, а это неплохо... Видимо грани "есть" только для плоских графов, или ещё для вложенных в ориентируемую поверхность(тор,крендель)?
Из подготовленного письма:
Так, я осознал свою глупость! Грани предложенного графа посчитаны неправильно!
Быстро нашел на ютубе обучающие видео на английском(3-летней давности). Ссылки не сюда. Помогло.
Так вот, всё,что надо было вспомнить - дуальность графов. И опус:
надо использовать "мягкость" графа: "покрутить", "повертеть" и минимизировать неустранимые пересечения рёбер на плоскости.
Пусть их количество будет

. В принципе именно в них и должны быть "дырки" поверхности рода

, куда граф приятно вложится.
Можно нужную поверхность склеить из 2-мерных клеток-многоугольников с количеством рёбер, равным степени соответствующей вершины. Есть гипотеза, что это минимальная (двусторонняя), в которую граф вложим... Можно посчитать эйлерову хар-тику уже этой поверхности (без края).
В такую вкладывались у меня

,

,
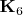
и тот граф по-выше. Я так же проверил для ещё четырёх:

с добавкой 8-и рёбер и
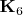
без одного ребра, и двух планарных, - работает.
В результате, если сохранить рёбра по швам склеек, получится некий граф, тоже вложенный в созданную поверхность;
пример случая для
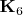
показал, что этот граф
не дуален
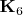
. Для планарных получалась сфера

.
Не знаю, будет ли это справедливо с графом со счётно-бесконечным количеством вершин и рёбер.
Если этот метод действительно работает, я наверняка изобрёл велосипед.



