Возрастающее число слагаемых в суммах по

и по

.
Ну знаете, при численном интегрировании слагаемых тоже немало...
Именно так. Если выражение истинно, скобка возвращает 1, если ложно - 0.
Ok, вот вам
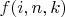
Код:
MF=Map();
f(i,n,k)={
my(sum1,sum2,sum3,factor1,res);
if(mapisdefined(MF,[i,n,k],&res),return(res));
if(i >=0 && i<2 && n==1 && k==0, sum1=1,sum1=0);
if(i >=0 && i<3 && n>1 && k>=0 && k<2^(n-1), factor1=1,factor1=0);
if(factor1==0, mapput(MF,[i,n,k],sum1);return(sum1));
if(i==h(n,k),sum2=1,sum2=0);
sum3=f(i,n-1,k\2);
res=sum1+sum2+sum3;
mapput(MF,[i,n,k],res);
return(res);
}
А, погодите, или вы имели в виду что вы на PARI
уже всё написали и оно долго считается?



