Ограниченно обратимое отображение

[Alexzord]

Изучаю задачу Дирихле: $-y'' + q(x)y = \lambda y, \quad y(0) = y(1) = 0$.
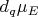
У нас есть некоторое отображение $\mu_E : E \rightarrow \mathbb{R}\times \ell_2$, where $E = \{q\in L_2: q(x) = q(1-x)\}$. Знаем, что его производная Фреше $d_q\mu_E$ из $E$ в $\mathbb{R}\times \ell_2$ задается таким образом

$$v \mapsto d_q \mu_E := (\langle 1, v \rangle, \langle g_n^2 - 1, v\rangle, n\geq 1)$$

где $g_n = g_n(q)$ - собственная функция для $q\in L_2$, $\mu = \mu(q) = \{\mu_n\}$ - последовательность собственных значений, а $\mu_E = \mu |_E$.

Мне надо показать, что $d_q \mu_E$ ограниченно обратимо всюду на $E$. Известно, что векторы $1, g_n^2 -1$ образуют базис $E$. В книжке написано, что из этого и следует, что $d_q \mu_E$ ограниченно обратимо. Я не могу понять, почему.

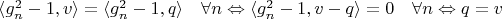
Инъективность понятна: $\langle g_n^2 - 1, v\rangle = \langle g_n^2 - 1, q\rangle \quad \forall n \Leftrightarrow \langle g_n^2 - 1, v-q\rangle = 0 \quad \forall n \Leftrightarrow q = v$ т.к. $1, g_n^2 -1$ базис $E$.

Помогите показать ограниченность в ту и в другую сторону.

Возможно, надо использовать вот это $g_n^2 = 1 - \cos 2\pi n x + O(1/n)$.

Норма на $\mathbb{R}\times \ell_2$ пусть такая же как просто на $\ell_2$: $\|(c_0, \{c_n\})\| = \sqrt{\sum_0^\infty c_k^2}$.