Добрый день! Помогите, пожалуйста! Есть уравнение

,

- матрица, размер

,

и

- вектора размером

.
В прямой задаче нужно найти вектор

, матрица

и вектор

- это экспериментальные данные. Известно, что в них есть погрешности. Из

и

можно получить правильные данные

и

умножением их поэлементно на некоторые поправочные коэффициенты

и

.

Я решаю обратную задачу, то есть мне известны компоненты матрицы

, вектора

и и модельного вектора

. Нужно найти поправочные коэффициенты

и

и минимизируемую функцию

(предельно допустимая погрешность аппроксимации экспериментальных данных). Также дан заданный порог точности в уравнениях

. Обозначается

.






Из этой системы нашла

(использую LPSolve - ПО для решения задач линейного программирования (ЗЛП)). Обозначила найденное

как

. Добавила в ЗЛП уравнение
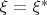
(найденное на предыдущем шаге значение). Вместо оптимизируемой функции указала каждый из параметров

и

. Устремляла их к минимуму и максимуму. Таким образом, нашла минимальные и максимальные значения каждого коэффициента

и

.



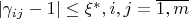

Т.е. в результате для каждого параметра

и

получила интервалы значений
![$[ymin_{ij}; ymax_{ij}]$, $i=\overline{1,m}, j=\overline{1,n}$ $[ymin_{ij}; ymax_{ij}]$, $i=\overline{1,m}, j=\overline{1,n}$](https://dxdy-01.korotkov.co.uk/f/8/6/6/8660ace1d8ea39c0991d6a23a2de5db582.png)
. Всего 30 интервалов (размерность - 5, 30 параметров: 25

и 5

).
Посоветуйте, пожалуйста, как дальше уточнять эти интервалы, по какому алгоритму. Мне кажется, что это 30мерный кубик, в котором ищется решение. Перебор не подходит. Потому что даже если задать 2 узла на каждом ребре (что вообще очень мало), получится

(миллиард) наборов. Может, какие-то параметры фиксировать по какому-то принципу, а какие-то варьировать?