Линейная зависимость векторов

[Sdy]

Начну с первого утверждения.
Утверждение.Пусть $(v_1, ... v_m)$ - такой кортеж векторов из векторного пространства $V$ над полем $F$, что для него выполнены следующие свойства:
(1)$\exists j : v_j \in span(v_1,...,v_{j-1})$.
(2)$\exists j : span(v_1,...,v_{j-1},v_{j+1},...,v_m) = span(v_1,...,v_m)$
Тогда этот кортеж линейно зависим.
Доказательство.
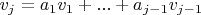
Пусть верно только (1). Тогда $v_j = a_1v_1 + ... + a_{j-1}v_{j-1}$, для некоторых скаляров из поля $F$.
Но тогда мы получаем, что $a_1v_1 + ... + (-1)v_j + ... + a_mv_m = 0$, когда все $a_i = 0$, а вот скаляр при $v_j$ равен $-1$, значит кортеж линейно зависим.
Пусть теперь верно (2).
Тогда для элемента из правой части равенства $v_1+...+v_j+...+v_m$ существуют такие скаляры для левой части, что $a_1v_1+...+a_{j-1}v_{j-1}+a_{j+1}v_{j+1}...+a_mv_m = v_1+...+v_j+...+v_m$. Но она обращается в нуль когда $a_j=-1$, значит исходный кортеж векторов линейно зависим. $\triangle$.

Вопросы.
Верны ли доказательства? Верно ли, что действительно достаточно только одного из этих условий для выполнения утверждения? Просто исходное утверждение звучит (частично) как if we consider a list $v_1, . . . , v_m$ of vectors such that either of the following statements are true:, которое я переводил как при выполнении обоих условий, но всё никак не мог в доказательстве задействовать второй пункт, решил доказать для каждого по отдельности.

[mihaild]

Sdy в сообщении #1420720 писал(а):

что $a_1v_1 + ... + (-1)v_j + ... + a_mv_m = 0$, когда все $a_i = 0$, а вот скаляр при $v_j$ равен $-1$, значит кортеж линейно зависим

Не очень понятно, что вы тут говорите про $a_i$ - они могут быть нулевыми, могут не быть. Важно что при $v_j$ коэффициент ненулевой.

В остальном всё правильно.

Sdy в сообщении #1420720 писал(а):

either of the following statements are true

Это переводится как "любое из следующих утверждений выполнено". Т.е. и надо было доказывать, что достаточно одного из этих условий (собственно эти условия эквивалентны: если добавление вектора не меняет линейную оболочку, то этот вектор принадлежит линейной оболочке имевшихся векторов).

[Sdy]

mihaild, спасибо за ответ.

mihaild в сообщении #1420725 писал(а):

Не очень понятно, что вы тут говорите про $a_i$ - они могут быть нулевыми, могут не быть. Важно что при $v_j$ коэффициент ненулевой.

Да, действительно, мне достаточно просто сказать, что линейная комбинация обращается в нуль, но при этом один скаляр нулю не равен.

mihaild в сообщении #1420725 писал(а):

Это переводится как "любое из следующих утверждений выполнено". Т.е. и надо было доказывать, что достаточно одного из этих условий (собственно эти условия эквивалентны: если добавление вектора не меняет линейную оболочку, то этот вектор принадлежит линейной оболочке имевшихся векторов).

Понял, спасибо.

[Sdy]

mihaild в сообщении #1420725 писал(а):

собственно эти условия эквивалентны: если добавление вектора не меняет линейную оболочку, то этот вектор принадлежит линейной оболочке имевшихся векторов

Пожалуй докажу и это утверждение.
Утверждение.
Пусть $(v_1, ... v_m)$ - кортеж векторов из векторного пространства $V$ над полем $F$, тогда условия
(1)$\exists j : v_j \in span(v_1,...,v_{j-1})$.
(2)$\exists j : span(v_1,...,v_{j-1},v_{j+1},...,v_m) = span(v_1,...,v_m)$
эквивалентны.
Доказательство.
Будем считать уже доказанным, что из (1) следует, что такой кортеж линейно зависимый и что из (2) следует, что такой кортеж линейно зависимый.
Тогда докажем, что из (1) $\Rightarrow$ (2). $\exists j : v_j = b_1v_1+...+b_{j-1}v_{j-1}+b_{j+1}v_{j+1} + ... + b_mv_m$.
Докажем, что любой элемент $span(v_1,...,v_m)$ является также элементом $span(v_1,...,v_{j-1},v_{j+1},...,v_m)$. Но любой элемент $span(v_1,...,v_m)$ имеет вид $u = a_1v_1+...+a_jv_j+...a_mv_m = a_1v_1 + ... + (b_1v_1+...+b_{j-1}v_{j-1}+b_{j+1}v_{j+1} + ... + b_mv_m) + ... + v_m$, а значит принадлежит $span(v_1,...,v_{j-1},v_{j+1},...,v_m)$.
Любой элемент $span(v_1,...,v_{j-1},v_{j+1},...,v_m)$ принадлежит $span(v_1,...,v_m)$ так как этому множеству принадлежат все линейные комбинации элементов $v_1,...,v_m$, а значит и те, где $a_j=0$, а остальные скаляры принимают произвольные значения.
Докажем, что (2) $\Rightarrow$ (1). Если выполнено 2, то кортеж линейно зависимый. Возьмем $j = \max\{1,...,m\} : a_j \ne 0$. Тогда, так как $b_1v_1+...+b_jv_j+...+b_mv_m = 0 \Rightarrow$ $v_j = c_1v_1+...+c_{j-1}v_{j-1}$, так как скаляр при нем не равен нулю, а все скаляры с номерами большими $j$ равны нулю. А значит $v_j \in span(v_1,...,v_{j-1})$

-- 15.10.2019, 02:50 --

mihaild в сообщении #1420725 писал(а):

Не очень понятно, что вы тут говорите про $a_i$ - они могут быть нулевыми, могут не быть. Важно что при $v_j$ коэффициент ненулевой.

А можно (1) так доказать? -
Возьмём $b_1v_1+...+b_{j-1}v_{j-1}+b_jv_j+...+b_mv_m$. Так как $v_j = a_1v_1+...+a_{j-1}v_{j-1}$, то положим $b_i = a_i$, тогда $(b_1v_1+...+b_{j-1}v_{j-1})+b_jv_j+...+b_mv_m = v_j+b_jv_j+...+b_mv_m$. Эта линейная комбинация обращается в нуль, при $b_j = -1 \wedge b_i = 0 \forall i > j$, значит $(v_1, ..., v_m)$ - линейно зависимы.