Не понимаю, почему нельзя пронумеровать все алгебраические числа способом, очень похожим на способ Виленкина, только со степенями "наоборот" в формуле.
Виленкин предлагает пронумеровать все алгебраические числа, (чтобы доказать счетность этого множества), (числа вида

или там
![$\sqrt[4]{3-\sqrt{5}}$ $\sqrt[4]{3-\sqrt{5}}$](https://dxdy-02.korotkov.co.uk/f/d/0/2/d02872ebd8c2b6610e2ff1530280f7be82.png)
)
следующим способом, (извиняюсь за такую огромную цитату из книги):
Цитата:
..отметим сначала, что каждое число рассматриваемого вида является корнем алгебраического уравнения вида

, (1)
где

и

— целые числа. Например,

корень уравнения

,

корень уравнения

. Иногда бывает очень трудно
написать уравнение, которому удовлетворяло бы число описанного выше вида, но тем не менее это всегда возможно.
Сначала перенумеруем все целые числа //"способом квадрата", т. е. в порядке 0, 1, -1, 2 и так далее
Номер целого числа

обозначим
через

[такая же буква в формуле, только жирная]. Каждому уравнению вида (1) поставим в соответствие число

[степени жирненькие]
(через

здесь обозначено
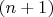
-е простое число). Например,
уравнению

ставим в соответствие номер
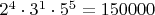
(потому что целое число

имеет номер 4,

— номер 1, а целое число

— номер 5). Теперь каждое уравнение получило свой номер,
причем разным уравнениям соответствуют разные номера (каждый
номер N единственным образом разлагается на простые множители,
то есть единственным образом задает числа
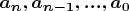
; этим же
числам соответствуют определенные целые числа

,
а тем самым и определенное уравнение

)
Не понимаю, почему нельзя сделать всё то же самое, только последняя формула будет такая:
Короче, возвести каждое простое число начиная с двойки в степень номеров целых чисел, соответствующих коэффициентам

и так далее до

, а не как Виленкин, начавший с возведения двойки в степень номера для

, потом тройку возвел в номер для

и так далее.
И поставить это число в соответствие каждому алгебраическому числу. Они же тоже будут уникальны и получится нумерация, разве нет?