если есть три хороших числа, то остальные заменим на одно, равное их НОДу.
Продолжая эту мысль: если домножить его на произведение трех плюс единица, то все четыре числа будут различными. Тогда задача сводится к нахождению семи взаимно простых чисел, которые формируют упомянутую четверку:

Вообще говоря, потребуется попарная взаимная простота только у чисел

, прочие могут, попарно, иметь общие делители, но только не в тройках.
По условию,

. Следовательно,

Для определенности, но без ограничения общности, можем считать, что

.
Следовательно,

.
Противоречие.Для двух чисел (хоть из ста, хоть из трех), как легко убедиться такими же рассуждениями, необходимо пять чисел:

. Тогда

. Как видно, здесь решение есть: мы можем использовать два любых взаимно простых числа

, тогда набор

, где
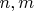
- произвольные целые, отвечает требуемому условию.
Например,

НОД всех, кроме второго, равен 21, всех, кроме первого - 100. В итоге в конечном наборе возникнут два числа 4321.



