склейка непрерывных функций

[beroal]

Прошу проверить доказательство.

Теорема. Пусть $X$ и $Y$ — топологические пространства. Пусть $I$ — множество. Пусть $\bar{X}: I\to \mathcal{P}(X)$ такое, что

• $\bigcup_{i\in I} \bar{X}(i) \supseteq X$
• и каждая $x\in X$ принадлежит $\bigcap_{i\in J} \bar{X}(i)$ и является внутренней точкой $\bigcup_{i\in J} \bar{X}(i)$ для некоторого конечного $J\subseteq I$.

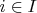
Пусть $f: X\to Y$ такая, что для каждого $i\in I$ сужение $f\restriction \bar{X}(i)$ непрерывно из топологии подпространства. Тогда $f$ непрерывна.

Доказательство. Пусть $x\in X$. Тогда существует такое конечное $J\subseteq I$, что $x\in \bigcap_{i\in J} \bar{X}(i)$ и $x$ является внутренней точкой $\bigcup_{i\in J} \bar{X}(i)$. Пусть $V$ — окрестность $f(x)$. Положим $\bar{U}(i) = (f\restriction \bar{X}(i))^{-1}[V]$ для $i\in J$. Тогда

$$f^{-1}[V] \supseteq \bigcup_{i\in J} \bar{U}(i).$$

Для каждого $i\in J$, так как $x\in \bar{X}(i)$ и $f\restriction \bar{X}(i)$ непрерывна, $\bar{U}(i)$ — окрестность $x$ в топологии подпространства на $\bar{X}(i)$. Поэтому существует такая $\bar{U}': J\to \mathcal{P}X$, что для всех $i\in J$ выполняется $\bar{U}(i) = \bar{U}'(i)\cap \bar{X}(i)$ и $\bar{U}'(i)$ — окрестность $x$ в $X$. Определим $U' := \bigcap_{i\in J} \bar{U}'(i)$, которое будет окрестностью $x$ в $X$. Получим

$$\bigcup_{i\in J} \bar{U}(i) = \bigcup_{i\in J} \bar{U}'(i)\cap \bar{X}(i) \supseteq \bigcup_{i\in J} U'\cap \bar{X}(i) = U'\cap \bigcup_{i\in J} \bar{X}(i),$$

и самое правое выражение — окрестность $x$ в $X$. Доказано.

В интернете я нашёл только теоремы, где все $\bar{X}(i)$ открытые или все они замкнутые.

[demolishka]

beroal, вроде бы верно.

[beroal]

demolishka в сообщении #1418350 писал(а):

beroal, вроде бы верно.

спасибо