Ищите близко лежащие точки по некоторому порогу. А далее ищите средние точки как описано тут:
http://ocrai.narod.ru/vectory.htmlВ дополнение можете поискать про алгоритмы оптимизации поллинии.
-- Ср сен 25, 2019 21:06:44 --А если выбрать в качестве параметров координаты промежуточных точек и воспользоваться тем же МНК?
Можно, но нужна пост обработка для разрешения вот таких вот случаев.
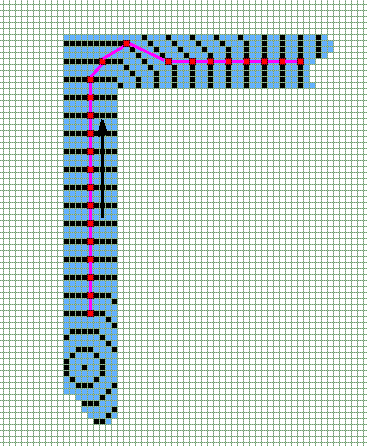
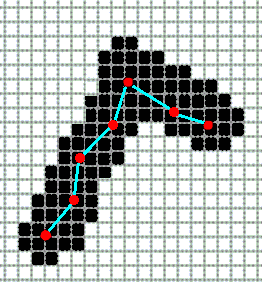
В статье что я дал выше описаны пути решения.
Если нужно могу ещё для 3-х мерного случая поискать, где-то у меня была статья.