Возник вопрос о доказательстве этого факта, скорее касающийся теории множеств.
Утверждение.Пусть

- сигма-алгебра подмножеств

,

- элементы сигма-алгебры,

- мера на этом измеримом пространстве.
Далее под

я понимаю счётное объединение подмножеств

, под

- счетное пересечение, то есть

всегда бежит по

Тогда если
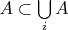
, то

.
Докажем вспомогательное утверждение.
Монотонность меры.
.
Доказательство.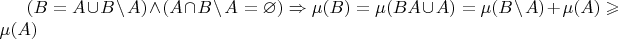
,
так как

.
Теперь
докажем исходное утверждение.
Сформируем вспомогательную последовательность множеств таким образом:
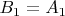
,
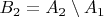
, ...,

,...
Докажем, сначала, что эти множества попарно не пересекаются.
Возьмем два произвольных множества

и

, для определенности, пусть
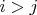
.

.

Пусть в их пересечении лежит

.
Но тогда, если

, то

не принадлежит

, получили противоречие.
Теперь нужно доказать, что

Сначала докажем, что

. Но действительно,

, значит любой элемент

входит в

.
Тогда докажем, что

.
Возьмем произвольный элемент с левой стороны. Он принадлежит какому-то из

. Пусть он принадлежит

. Но

, значит исходное включение доказано.
Осталось доказать, что

.
Возьмём элемент с левой стороны. Он принадлежит какому-то из

.
Предположим, что он не принадлежит правой стороне. Но тогда он не принадлежит ни одному из

. (Ведь тогда он не принадлежит
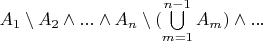
).
Получили противоречие.
Но тогда

. Так как
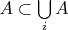
, то тогда

.
Но вследствие монотонности

, где последнее неравенство верно из-за того что

.
Значит утверждение доказано.
Вопросы.Больше всего меня тут интересует, правильно ли (и главное, строго ли) я доказал, что

? Во всей просмотренной литературе по теории вероятности данное предположение принимается на веру без доказательства, поэтому нет возможности самопроверки. Причем оно вот прямо кажется интуитивно понятным (и видимо поэтому везде опускается как упражнение), но у меня возникли большие временные трудности с его доказательством.