Ну хорошо, допустим мы выяснили, что множество рациональных чисел имеет дырки, не обращаясь к конкретным примерам.
Допустим мы ввели концепцию сечения Дедекинда, определили, что такое иррациональное число.
Но как доказать, что множество всевозможных сечений - является множеством точек на оси и заполняет всю ось без дырок?
То есть как доказать, что точке соответствует одно сечение, а одному сечению - одна точка?
Что, если одно сечение определяет не одно число, а некоторое множество?
К примеру сечение
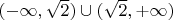
определяет не

, а некоторую сущность

.
Под символом

- подразумевается некоторая сущность, не являющаяся ни отрезком, ни интервалом, а является неким множеством - микроконтинуумом, не содержащим рациональных чисел.
И вот иррациональное число отождествляется с точкой на оси, и мы думаем что заполнили все точки на оси, а на самом деле мы пропустили бесконечное множество точек микроконтиннуума.
Можете ли вы гарантировать, что не существует никакого геометрического парадокса, который заставит ввести такие множества типа микроконтинуума.
Парадокс существует, называется вторая проблема Гильберта. Выход из парадокса - строгое, без рассуждений следование аксиоме, суть которой в том, что последовательность действительных чисел непрерывна, а числовая ось - "без дырок"
В принципе Ваши "невидимые" числа чем-то похожи на бесконечно малые, которые хоть и отличны от нуля, но точное значение этого отличия в математике неопределимо. Уже в самом понятии бесконечно малых заложен абсурд, а значит их существование под вопросом (как может существовать абсурдный математический объект!), и при этом бесконечно малые, это основа анализа. Другими словами, бесконечно малые на оси, это "дырки" в пространстве (в одномерном, в случае оси), т.е. куда бы вы ни "ткнули пальцем" на числовой оси - всегда попадете в действительное число, а между соседними числами, которые отличаются на бесконечно малую величину, вы "ткнуть" не сможете по определению, хотя это отличие не нулевое. Налицо (исходя из аксиомы о непрерывности последовательности действительных чисел) отсутствие пространства между соседними числами.
Между прочим, отсюда вытекает и дискретности времени

...