Я сейчас пытаюсь освоить функан по классическому учебнику Колмогорова и Фомина. Я привожу здесь свою попытку решения упражнения оттуда, чтобы убедиться в его правильности:
Цитата из учебника:
Цитата:
Это явление характерно для бесконечных множеств. Действительно, в п. 2 (свойство 3) мы показали, что из всякого бесконечного множества М можно выбрать счетное подмножество; пусть

такое подмножество. Разобьем его на два счетных подмножества

,

и установим между

и

взаимно однозначное соответствие. Это соответствие можно затем продолжить до взаимно однозначного соответствия между множествами

и (Л/ \ .4) = М и

, отнеся каждому элементу из

сам этот элемент. Между тем множество
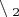
не совпадает с
M, т. е. является собственным подмножеством для
М. Мы получаем, таким образом, следующее предложение:
Всякое бесконечное множество эквивалентно некоторому своему собственному подмножеству.
Это свойство можно принять за определение бесконечного множества.
Упражнение. Доказать, что если

— произвольное бесконечное множество и

счетно, то

.
Я провел доказательство по индукции:
1. Пусть задано произвольное бесконечное множество

. Согласно доказанному выше утверждению,

эквивалентно некоторому своему собственному подмножеству

, где

- некое непустое подмножество. Пусть в него входит элемент

. Без потери истинности утверждения можем заменить элемент

на элемент

.
2. Пусть утверждение доказано для некоторого произвольного бесконечного множества
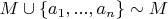
.
Докажем утверждение для

. Оно эквивалентно множеству

. (Поставим в соответствие элементу

элемент

). А как доказано в п.1, оно эквивалентно множеству

. В силу транзитивности определения эквивалентности, имеем:

.
Шаги доказательства по индукции проводятся счетное число раз, отсюда имеем доказательство

для счетного

.



