Попробую продолжить построение, предварительно выписав, что на данный момент мне
известно и что я умею доказывать:
Аксиоматика Пеано:
1)

- натуральное число.
2)Если

- натуральное, то

- натуральное.
3)Из

.
Тут же с помощью контрапозиции

и с помощью аксиомы подстановки

.
4)Не существует такого натурального

.
5)Если

- некоторое свойство, верное для натурального числа, это свойство верно при

и для всякого натурального числа

из того что оно верно для

следует, что оно верно для

, тогда это свойство верно для любого натурального числа.
Сложение натуральных чисел было определено рекурсивно так:
1)

.
Пусть мы умеем находить сумму

, тогда сумма

.
Далее доказали следующие соотношения (далее

- натуральные числа):
1)

- натуральное число.
2)

.
3)

.
4)

.
5)

.
6)

.
7)Если

.
8)

Определили положительное число, как натуральное, неравное нулю.
9)Если

- положительное и

- натуральное, то

- положительное число.
10)

Начали вводить порядок на натуральных числах как:

.

.
Необходимо доказать следующий набор утверждений: (далее

- натуральные числа)
a)

b)

c)

d)

e)

f)
 Докажем
Докажем их по порядку (далее

- натуральные числа).
a b
bЕсли

, тогда

и

, но тогда

, что означает, что

.
cЕсли

, то

и

. Значит

, но тогда

, а значит

и

.
dДля начала пусть

. Тогда

, а в силу аксиомы подстановки

.
Теперь пусть

. Тогда

, следовательно

, что означает по определению, что

.
eПусть, сначала
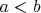
, значит

и

. В силу аксиомы подстановки и определения сложения, получаем, что

, значит

.
Теперь нужно доказать, что

.
Воспользуемся контрапозицией, докажем, что

.
Для начала, предположим, что

. Так как

, то

, пришли к противоречию.
Осталось показать, что

. Но это так как

, то все доказано.
fПросто по определению,

, причем если

, то

, что неверно.
Теперь, пусть

, причём

. Предположим, что при этом

. Но тогда сразу (по

)

, что неверно. Значит, по определению,

.
Вопросы.1)Хотелось бы, удостовериться, что во-первых я нигде не ошибся, а во-вторых - не вылез за рамки доказанных уже свойств, принятых аксиом и знания о том, что такое равенство как отношение.
2)Пусть

. Я делаю вывод, что

. Это аксиома подстановки тут работает же?