Есть вопросы по упражнениям на страницах 44 и 45 следующей книги.
Takeuti, Gaisi, and Wilson M. Zaring.
Introduction to Axiomatic Set Theory. 2nd ed. New York: Springer-Verlag, 1982. Print. Graduate Texts in Mathematics 1.
Цитата:
(3)

.
(4)

.
В упражнении 3, если выбрать

, то

, и

явно ложно. Если

непуст, то, полагаю, можно найти цепочку

, ведущую из

в

, и исходя из транзитивности по индукции доказать

, и тогда

истинно, но почему бы не написать просто

?
В упражнении 4, если выбрать

и

, то следует

. Возможно, имелось в виду
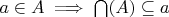
?
Цитата:
(4)

.
Если выбрать

, то
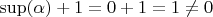
. (Мне кажется, по идее,

надо считать предельным ординалом.)
Цитата:
Определение 7.22.

.
Цитата:
Определение 7.27.
![$K_\mathrm{I} \overset{\Delta}{=} \{\alpha\mid \alpha = 0 \lor (\exists\beta)[\alpha = \beta + 1]\}$ $K_\mathrm{I} \overset{\Delta}{=} \{\alpha\mid \alpha = 0 \lor (\exists\beta)[\alpha = \beta + 1]\}$](https://dxdy-02.korotkov.co.uk/f/5/4/0/54075f50705e3b24e18e72426cb56e3a82.png)
.

.
Заглавными латинскими буквами обозначаются классы, греческими буквами обозначаются ординальные множества. Пустое множество обозначается как

. Класс всех множеств обозначается как

. Класс всех ординальных множеств обозначается как

. Предикат

значит, что

транзитивен.