Если повороты проводятся строго последовательно, то нужно тупо перемножить три матрицы (или кватерниона) известного вида. Если же повороты можно проводить одновременно с произвольными (пусть просто разными) угловым скоростями, то задачка становится интересней. Можно что-то оптимизировать...
Можно вращать последовательно, но сейчас они крутятся одновременно. Я не предполагал, что это изменит решение. Кстати идея с получением двух матриц по паре троек углов, описывающих предыдущее и последующее состояния сервов провалилась. Опишу задачу в большем количестве деталей. На "целевой" площадке стоят датчики (магнитометр, акселерометр и гироскоп). Стоят весьма произвольно таким образом, что мне неизвестен переход от их локальной системы к системе сервов. Да и что собой представляет система сервов весьма смутно представляю - просто я выбрал их крайние положения за нули, а противоположные крайние положения за 360, 360 и 180 соответственно. С датчиков я могу снимать показания в любой момент времени. Показания - сыроваты (некалиброванные) и оттого не совсем точные. Цель - получив некоторое множество показаний (сейчас речь про акселерометр, который в любом установившемся состоянии сервов будет показывать вектор, норма которого должна быть 9,81) в каком либо положении, усреднив их и скрепя сердце поверив этому усреднению - остальные показания вычислять из поворотов целевой платформы и сверять с реальными показаниями датчиков.
Использовав следующую матрицу:

подставляя в качестве
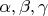
углы, которыми я описываю состояния сервов - я для этих состояний по этой формуле нашел матрицы якобы им соответствующие, нашел матрицу, описывающую поворот от первой ко второй. Применил этот поворот к вектору акселерометра, соответствующего первому состоянию. И должен был бы по задумке таким образом предугадать вектор акселерометра, соответствующий последующему состоянию. Но не тут то было.
Ко мне закрадываются смутные подозрения, что я абсолютно неправильно представляю себе систему координат серво-робота, выражая ее через углы поворота сервов каждый вокруг своей физической оси
Еще один умный человек предложил мне покрутить каждым сервом по отдельности. Снимая при этом показания с гироскопов мы можем получить ось вращения в локальной системе гироскопа (предположительно, но не уверен на все три датчика одна локальная система) и так для каждого серва. То есть получим какой-то с натяжкой сказать базис. Но я пока не переварю, что с ним дальше делать