Здравствуйте! Нужно найти максимальное количество ребер у двудольного графа. Я рассуждаю следующим образом:
Пусть
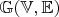
- граф, где

- конечное множество всех вершин, а

- множество всех неупорядоченных пар.

. Пусть одна из долей имеет

вершин, тогда другая имеет

вершин. Т. к. в графе пара вершин может соединяться только одним ребром и в графе нет петель, то очевидно, что количество ребер равно

. Возьмём производную по m и приравняем к нулю. Получается

или

. Подставим теперь это в формулу количества рёбер и получим ответ

.
Возникает вопрос: а если

нечётно? То есть не представляется в виде

. На ум приходит положить

, но будет ли это максимумом? И если да, то почему?



