Оценка погрешности интерполяции с равноотстоящими узлами

[andreyka]

В книгах приводится оценка $\|P_n-f\|\le \left\|\frac{f^{n+1}(\xi)}{(n+1)!}\right\| \|\omega_{n+1}\|$, где $\xi \in (x_0, x_n)$ и $\omega_{n+1}(x)=(x-x_0)(x-x_1)\dots(x-x_n)$.
В случае равноотстоящих узлов $\omega_{n+1}(x)=(x-x_0)(x-x_0-h)(x-x_0-2h)\dots(x-x_0-nh)$, где $h=\frac{x_n-x_0}{n}$.
Как обычно на практике оценивают погрешность в случае с равноотстоящими узлами? Находят произведение $(x-x_0)(x-x_0-h)(x-x_0-2h)\dots(x-x_0-nh)$ для конкретной точки $x$ или есть более удобные формулы?

[Someone]

andreyka в сообщении #1412315 писал(а):

для конкретной точки $x$

В вашей формуле, вообще-то, норма написана, а не значение.

[andreyka]

Ой, сначала начал писать для точки, потом решил для нормы и все спутал.

Для точки $|P_n(x)-f(x)| = \frac{1}{(n+1)!} \left|f^{(n+1)}(\xi)\right| |\omega_{n+1}(x)|$, где $x, \xi \in (x_0, x_n)$

Для нормы $\|P_n-f\| \le \frac{1}{(n+1)!}\left\|f^{(n+1)}\right\| \|\omega_{n+1}\|$, где нормы рассматриваются по интервалу $(x_0, x_n)$

[Someone]

andreyka в сообщении #1412384 писал(а):

нормы рассматриваются по интервалу $(x_0, x_n)$

Наверное, всё-таки на отрезке $[x_0,x_n]$.

andreyka в сообщении #1412315 писал(а):

Находят произведение $(x-x_0)(x-x_0-h)(x-x_0-2h)\dots(x-x_0-nh)$ для конкретной точки $x$ или есть более удобные формулы?

А какая проблема с вычислением произведения? У Вас $n=10^{10^{10}}$?
Проблема может быть с оценкой $\lvert f^{(n+1)}(\xi)\rvert$, поскольку $\xi$ неизвестно.

[andreyka]

Someone в сообщении #1412436 писал(а):

Наверное, всё-таки на отрезке $[x_0,x_n]$.

Точка $\xi$ внутренняя, потому что в обосновании формулы используется теорема Ролля. Крайние точки $x_0, x_n$ -- узловые, поэтому погрешность и $\omega_{n+1}$ там обращаются в 0 и нет смысла в этих точках оценивать норму $\omega_{n+1}$. Наверно, в случае экстраполяции, когда $x$ крайняя, надо учитывать значение $\omega_{n+1}(x)$.

Someone в сообщении #1412436 писал(а):

А какая проблема с вычислением произведения? У Вас $n=10^{10^{10}}$?

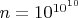
Просто подумал, что есть какая-то формула для оценки нормы $\omega_{n+1}(x)$ на всем интервале.

Была идея так оценить. Возьмем самый плохой случай: $x$ принадлежит самому крайнему отрезку разбиения. Тогда расстояние от $x$ до какого-то соседнего узла не больше $h/2$, а до другого соседнего не больше $h$, где $h$ шаг разбиения. До следующего узла не больше $2h$, до следующего за ним не больше $3h$ и т.д до самого дальнего узла не более $(n-1)/h$. Тогда получим $\|\omega_{n+1}\| \le \frac{(n-1)!}{2}h^{n+1}$. 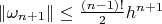Правильно? Насколько это грубая оценка?

[andreyka]

Ошибка. До самого последнего узла не более $n/h$, поэтому $\|\omega_{n+1}\| \le \frac{n!}{2}h^{n+1}$

-- 28.08.2019, 19:37 --

Пусть отрезок [0,1] и n=5. Тогда $\frac{n!}{2}h^{n+1}=\frac{5!}{2}(1/5)^{6}=0.00384$.
Пусть отрезок [0,10] и n=5. Тогда $\frac{n!}{2}h^{n+1}=\frac{5!}{2}2^{6}=3840$.
Как-то странно масштабируется

[worm2]

Не странно, всё правильно.
Если мы теперь во втором отрезке используем ту же функцию, что и в первом, растянутую в 10 раз ($f(x/10)$), то для неё интерполяционный многочлен, разумеется, будет тем же, но также растянутым в 10 раз, а $n+1$-я производная уменьшится ровно в $10^{n+1}$ раз, и в итоге получится в точности та же оценка погрешности.