Помогите с решением системы уравнений.

[QQQQwwww]

(1) и (2) - система.
$x^2y+xy^2-2x-2y+10=0$ (1)
$x^3y-xy^3-2x^2+2y^2-30=0$ (2)
Умножив первое на 3 получаю.
$3(x+y)(xy-2)=-30$ (3)
$(x^2-y^2)(xy-2)=30$ (4)
Сложив (3) и (4) получил.
$(xy-2)(x+y)(x-y+3)=0$
Понимаю, что каждая из 3х скобок может равняться нулю, но почему-то не удается решить уравнение (1) или (2), подставив в них выраженное значение одной из переменных.
Помогите пожалуйста.

[angor6]

QQQQwwww

QQQQwwww в сообщении #1411298 писал(а):

... почему-то не удается решить уравнение (1) или (2), подставив в них выраженное значение одной из переменных.

Что именно Вам не удаётся?

[Pphantom]

QQQQwwww в сообщении #1411298 писал(а):

Понимаю, что каждая из 3х скобок может равняться нулю

Ой ли? Допустим, нулю равна первая скобка. Каким образом тогда в правой части уравнения (3) (или (4)) может получиться что-то, отличное от нуля?

Ну и в самом деле распишите детальнее те действия, которые сделать не удается.

[QQQQwwww]

angor6
Pphantom
Ага, вот первая ошибка: только третья скобка может равняться нулю.
Тогда: $x=y-3$
Подставлять в (3)/(4) бессмысленно, т. к. все сократится.
Подставлю в (1) уравнение, получу:
$2y^3-9y^2+5y+6=0$
Оно не решается в целых числах. (ответ на задачу $x=-4$, $y=-1$)

[wrest]

QQQQwwww в сообщении #1411302 писал(а):

Подставлю в (1) уравнение, получу:
$2y^3-9y^2+5y+6=0$

Один из коэффициентов неверный.

[Pphantom]

QQQQwwww в сообщении #1411302 писал(а):

Ага, вот первая ошибка: только третья скобка может равняться нулю.

Да, и это можно было бы обнаружить, просто разделив (4) на (3).

QQQQwwww в сообщении #1411302 писал(а):

Подставлю в (1) уравнение, получу:

Проверьте еще раз.

[QQQQwwww]

Pphantom
wrest
А, вижу, не 6, а 16.
Тогда все сходится.
А можно решить эту систему, не прибегая к решению уравнения третьей степени? (и не наугад)

[wrest]

QQQQwwww в сообщении #1411306 писал(а):

А можно решить эту систему, не прибегая к решению уравнения третьей степени? (и не наугад)

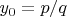
По теореме о рациональных корнях многочлена, для $2y^3-9y^2+5y+16=0$ если есть корень $y_0=p/q$ то $p$ -- делит $16$ а $q$ -- делит $2$, соответственно, если корень предполагается целым то он делит свободный член. Так что перебираете делители $16$ ($\pm 1, \pm 2, \pm 4, \pm 8, \pm 16$), если корень не нашелся значит целых корней нет, начинаете перебирать дроби, если корень не нашелся значит он не рациональный...
Перед этим замечаете что положительных корней нет, так что перебираете только отрицательные, и удача вас настигает на первой же попытке!

[Pphantom]

QQQQwwww в сообщении #1411306 писал(а):

А можно решить эту систему, не прибегая к решению уравнения третьей степени? (и не наугад)

Тут это не слишком надо. Похожесть структуры уравнений видна сразу, идея разложить то, что можно, на множители тут напрашивается, а дальше все очевидно. Итоговое кубическое уравнение в самом деле убивается теоремой Безу, хотя, если не поможет, есть формула Кардано.

[QQQQwwww]

Pphantom
wrest
Спасибо большое!
Тему считаю закрытой.