Извините за небольшое мое изчезновение. Если честно, я задумался над тем, что написал worm2 и не хотел ничего писать пока мое представление продолжало формироваться.
Worm2 написал правило №2. В нем для меня приятная неожиданность. Пытаясь раскусить алгоритм самостоятельно, я несколько раз подозревал, что здесь может быть замешан дистрибутивный закон, но где - понять не повезло. Правило №2 - это натуральный дистрибутивный закон, ведь так? Значит, нет сомнений что

,

,

имеют общий делитель. И тут мысль: если
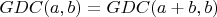
, тогда

. И снова,
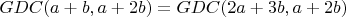
. И так до бесконечности! Вывод: один и тот же НОД содержится в начальном "дистрибутивном выражении" и в эквивалентном ему, путь к которому лежит через произвольное количество повторений. Но при этом разрядность числа будет расти до бесконечности.
И вот есть два бесконечно больших числа. Ты уверен, что их НОД - это та самая двоечка(например) с которой ты начинал? Тут я приуныл. Самое очевидное решение было начать в ручную прописывать этот сценарий на конкретных числах. Допустим

, а
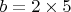
. Вот:

Да, числа большие, а значит делителей больше, а значит нельзя исключать, что в разложении этих чисел на простые множители общими окажутся не только 2-ки, но еще какие-то делители и НОД изменится. Но проверяем и убеждаемся, что во всех случаях НОД - это 2. Как такое возможно? - Только в одном случае - когда множители при коефициентах 2 - это два взаимно простых числа. Не простых, а взаимно простых! Шок! Вот это математика! Как возможно, что всегда эти числа оказываются взяимно простыми? Посмотрев еще раз на выражения, я заметил, что

- это тоже самое что

. Попробую сделать второй вывод... Если

и

- взаимнопростые числа, то

и

также будут взаимно простыми числами. Если я нигде не ошибся, то именно этот последний вывод я считаю ключом к доказательству обсуждаемого алгоритма.
А теперь вернемся к тому, что написал worm2. Когда мы уяснили правило 2 и у нас нет более никаких сомнений, подобных описанному выше, то давайте допустим, что правило работает и в обратную сторону, тоесть будем уменьшать делимое, отняв от него делитель. Вообще, чем вызван этот шаг? Да просто два аргумента не поделились нацело и второе правило для нас - как единственное утешение. По-крайней мере, уменьшая делимое мы не теряем НОД, а там, может и более удачное соотношение чисел подвернется и разделятся они! Но тут же понимаем, пока разность делимого и делителя больше делителя не разделятся они. Потому что не в делителе причина неделимости. Остаток, который скрывается за всеми вычитаниями - это он не кратен делителю. Наконец, докопались мы до остатка. Для нас уже не принципиально, что это называется остатком. Главное, что НОД остатка и делителя равен НОД делимого и делителя. Абстрагируемся от предыстории и снова пытаем удачу деля больший аргумент на меньший. Если не в этот раз то в следующий должно разделится без остатка. Тогда и пригодятся те слова из Зайцева, что при делении нацело делитель есть НОД.
Кстати, пишите данные книг полностью
В.В. Зыйцев, В. В. Рыжков, М. И. Сканави - Элементарная Математика(Издательство "Наука", Москва 1974г.
А. Г. Цыпкин - Справочник по математике для средних учебных заведений(Изд-во "Наука", 1988г)
Г. Дэвенпорт - Высшая Арифметика. Введение в теорию чисел.(перевод с английского, изд-во "Наука", 1965г.)
Чего можно умудриться не понять в таком изложении стандартной версии алгоритма Евклида --- загадка.
Прошу понять меня правильно, я не имел в виду бросить тень на эти чудесные книги. Я их по-прежнему ценю. Только Дэвенпорта я читаю в электронном варианте, а чтобы купить остальные книги мне пришлось поехать в другой город на книжный базар. Дело в том, что этим алгоритмом, я занялся вообще не по своей воле. Я наткнулся в специальной литературе на слова "операция вычета по модулю". Так как я серьезно отношусь к этой литературе, то не могу расчитывать на усвоение материала, не понимая математического аппарата, на который этот материал опирается. Вот траектория, которая меня завела в эту тему: вычеты по модулю - сравнение по модулю - деление с остатком - алгоритм Евклида. Естесственно, нервничаешь ибо всегда хочется быстрее.

Возможно, у кого-то есть комментарии по теме - милости прошу.