Хотел бы попросить проверить доказательство следующего утверждения.
Утверждение.Произведение двух нижнетреугольных матриц есть матрица нижнетреугольная.
Для начала введём следующее
Определение.Квадратная матрица

называется нижнетреугольной, если

.
Доказательство.Пусть имеется две нижнетреугольные матрицы
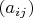
и

.
Матрицу, получающуюся в результате произведение этих матриц обозначим как
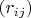
.
Значит нам нужно доказать, что
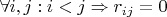
.
Рассмотрим произвольный элемент матрицы

. Из определения матричного произведения он равен:
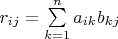
.
Докажем, что он равен нулю, как только
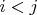
.
Тогда для любого из слагаемых, образующих в сумме такой элемент возможны три варианта:
1)

. Но так как

,то это слагаемое равно нулю.
2)

.

, значит и такое слагаемое будет равно нулю.
3)

.

, следовательно и это слагаемое будет нулевое.
Но это означает, что как только
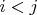
, так

, а значит матрица

- нижнетреугольная.

.



