А почему

в
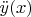
и
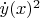
разные? Как это представить? Неужто это не одни и те же

?
На это, на самом деле, можно смотреть с разных сторон.
Вторая производная определяется как производная от производной. Если расписать через пределы, то

И это получается вложенный предел: сначала переходим к пределу в первой производной, а потом во второй. Разности

в первой и второй формуле независимы, но мы привыкли обозначать их одним и тем же символом, так что здесь некоторая путаница. Давайте запишем явно:

Итого

C этой точки зрения,

во второй производной - это произведение
разных независимых dx, и поэтому сокращать его с

, которое является настоящим квадратом, некорректно.
Либо можно доказать, что дельты можно принять одинаковыми, т.е. вторая производная есть предел второго разностного отношения

В этом случае проблема возникает не с

, а с
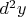
: здесь существенно, что значения

,
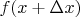
,

берутся в
равноотстоящих друг от друга точках, потому что мы условились, что дельты равны. Поэтому
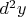
становится зависимым от выбора независимой переменной: значения

, соответствующие равноотстоящим

, дают вообще говоря не тот результат, что значения

, соответствующие равноотстоящим значениям какой-нибудь другой переменной

.
С этой точки зрения, проблема в том, что
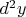
в

и

говорят о разных предельных переходах.



