Мера иррациональности 
вещественного числа

определяется через множество
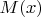
всех чисел

, таких, что неравенство

имеет лишь конечное число решений в целых числах

и

. Она есть нижняя грань множества
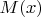
: то есть

. Если

, то полагают по определению

.
Пусть

– положительное натуральное число

. Положим

в определении меры иррациональности числа

и обозначим через

множество всех чисел

, таких, что неравенство

имеет лишь конечное число решений в целых числах

и

. Тогда величину

можно назвать мерой иррациональности числа

по основанию

. Если

, то положим по определению

. При

получаем меру двоичой иррациональности, при

– меру троичной иррациональности и т. д. При

получаеся мера десятичной иррациональности. Ясно, что

. Возникает ряд естественных задач для подобных мер иррациональности.
Задача 1. Чему равна мера двоичной иррациональности для рациональных чисел, не являющихся двоично-рациональными?
Задача 2. Вычислить

для чисел

,

и т. д., то есть для всех иррациональных корней из целых чисел.
Задача 3. Вычислить

для числа

(основание натурального логарифма).
Задача 4. Вычислить

для числа

(площадь единичного круга).
Имеется связь между

и функциями

и

, определёнными в теме "
Задачи о доле единиц в двоичной записи чисел". Если

, то

. Если

, то

.
|
i |
Последняя фраза изменена по просьбе участника. |