Хочу в первом приближении понять смысл терминологии дифференциальной геометрии на примере многообразия
, вложенного изометрически в евклидово пространство
:
1. Если сказано, что существует многообразие
, то это значит, что речь идет о какой-то поверхности, точки которой уже адресованы (имеют координаты в виде пары чисел
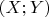
), причем бесконечно близким координатам соответствуют бесконечно близкие точки. Свойство бесконечной близости точек многообразия уже существует еще до определения понятия расстояния между ними. Хотя у нас уже есть координаты точек, расстояния на многообразии еще нет. Форма поверхности не определена;
2. Если сказано, что многообразие дифференцируемое, то это значит, что поверхность гладкая;
3. Если на многообразии задана связность, то это значит, что на этой поверхности определено правило локальной параллельности. В общем случае на криволинейной поверхности возможно говорить только о параллельности бесконечно близких касательных векторов, так что невозможно ничего сказать об отношении параллельности таких векторов в точках с конечной разностью координат. Если задана связность, то мы можем построить цепочку векторов, сохраняющих свойство параллельности в каждой точке, т.е. осуществить параллельный перенос вектора. При этом свойство параллельности именно локальное: если параллельно перенести вектор из точки А в точку В, то в этих точках не будет два параллельных вектора, т.к. вообще результат переноса "не потенциален" и зависит от пути переноса, а не только от начальной и конечной точек. Из-за зависимости результата переноса от пути переноса глобальная параллельность не определена. При параллельном переносе вектор по определению не меняется, т.е. связность говорит о том, что значит "неизменность объекта при перемещении", т.к. на не плоских многообразиях это не очевидно. Опираясь на это определение "неизменности", можно уже говорить об изменении объекта при перемещении вдоль пути, т.е. о производной вдоль пути;
4. Связность позволяет сразу построить геодезические линии, которые определяются, как линии, всюду касательные параллельно переносимому вектору. Любой вектор, переносимый вдоль геодезической линии, сохраняет с ней неизменный угол (в частности, нулевой), но о постоянстве угла в общем случае можно говорить только после определения расстояния на многообразии. Связность позволяет соединить все точки многообразия геодезическими линиями (которые при этом не имеют смысла кратчайших), однако форма поверхности все еще не определена;
5. Один из самых простых типов связности - риманова связность, при которой правило локальной параллельности векторов определяется так: если на нашей поверхности даны два бесконечно близких касательных вектора А и В, то они считаются параллельными, если проекция вектора В (в
) на касательную плоскость вектора А параллельна А. Определение этой связности, похоже, требует, чтобы форма поверхности уже была известна, а форма поверхности определяется метрикой. Т.е. риманова связность целиком определяется метрикой (и наоборот);
6. Если на многообразии задана метрика, то это значит, что задано правило локального вычисления расстояния между бесконечно близкими точками. С этого момента поверхность приобретает вполне определенную форму. Геодезические становятся кратчайшими, что не противоречит их определению, как линий, касательных к параллельно переносимому вектору, т.к. связность и метрика на римановом пространстве получаются друг из друга.
Все, что я написал - это вовсе не утверждения, а уровень моего понимания вопроса на текущий момент. Хотелось бы узнать, насколько правильно я это себе представляю.
называется многообразием, если каждая его точка имеет открытую окрестность, допускающую непрерывное 1-1-отображение (называемое координатным) на открытое множество в 