Описываются подходы и примеры, которые могут быть полезны для решения задачи.
Распределения на
![$[0,1]\times[0,1]$ $[0,1]\times[0,1]$](https://dxdy-03.korotkov.co.uk/f/e/6/4/e64d7b6f9e262f17f34c09862141f55b82.png)
-квадрате для простоты и наглядности будем представлять плотностью распределения вероятностей

, имея в виду возможность использования

-функции Дирака. Впрочем, все нижеизложенное легко перевести на язык функций распределения или вероятностной меры.
Задача:

,
где множество

определено условиями:

![$ f_X(x) =\int _0^1 f(x,y)dy=1 (x\in [0,1]) , f_Y(y) =\int _0^1 f(x,y) dx =1 (y\in [0,1]) $ $ f_X(x) =\int _0^1 f(x,y)dy=1 (x\in [0,1]) , f_Y(y) =\int _0^1 f(x,y) dx =1 (y\in [0,1]) $](https://dxdy-01.korotkov.co.uk/f/c/f/0/cf0ea8f593247af7da2e2d52e41752ab82.png)
.
Учитывая, что

,
можно записать эквивалентные постановки задачи:

;
![$\int_0^1[\int _0^x yf(y|x)+x\int _x^1 f(y|x)]dy dx \to \max_{f \in \Omega_2 (\rho)} $ $\int_0^1[\int _0^x yf(y|x)+x\int _x^1 f(y|x)]dy dx \to \max_{f \in \Omega_2 (\rho)} $](https://dxdy-01.korotkov.co.uk/f/0/b/3/0b3c11a2a14f9ea8e4c4cabcbbd2f68082.png)
.
Пусть

(не производная), причем

, тогда

![=\max_{ \rho'(x)} \int _0^1 \max_{ p,,y_1,y_2} [(1-p(x)) \min \{x,y_1(x)\} +p(x) \min \{x,y_1(x)\} ] dx$ =\max_{ \rho'(x)} \int _0^1 \max_{ p,,y_1,y_2} [(1-p(x)) \min \{x,y_1(x)\} +p(x) \min \{x,y_1(x)\} ] dx$](https://dxdy-02.korotkov.co.uk/f/d/9/d/d9d5990cc683c5620d39dabe60c3972282.png)
,
где

(максимумы достигаются).
Переход к последнему соотношению сделан на основе теоремы Каратеодори, при этом механизм нахождения точек

в принципе понятен.
Мы видим, что при каждом значении

оптимальная в классе

функция распределения

(по крайней мере, одна из) дискретна и имеет не более двух точек роста (распределение двухатомное). Другими словами, если на
![$[0,1]\times [0,1]$ $[0,1]\times [0,1]$](https://dxdy-04.korotkov.co.uk/f/7/0/7/70719255eeec7e456629f50f69bce88a82.png)
-квадрате отметить точки с ненулевой плотностью вероятности, то они образуют такие множества, которые будут пересекаться не более чем в двух точках с любой «вертикальной» прямой и с любой «горизонтальной» прямой.
Теперь, если разбить квадрат на

квадратиков (называем точками), к такому же заключению можно придти относительно числа ненулевых точек в каждом столбце и каждой строке квадрата. Множество из
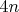
точек может быть разбито на

прямоугольников, в каждом из которых диагональные вершины (пусть главной диагонали) имеют одинаковые вероятности

, а побочной диагонали

Этот же факт непосредственно может быть установлен из теоремы Каратеодори (с учетом теоремы Рисса о распределениях): имеем множество распределений с
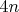
ограничениями (

по вертикали,

по горизонтали и одно на корреляцию), а также из рассмотрения сформулированной задачи как задачи ЛП. Следовательно, искомый максимум достигается на
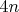
-атомном распределении. Анализ свойств экстремального распределения подсказывает, что в экстремальном случае точки будут расположены на диагоналях квадрата (такую конфигурацию точек будем называть - диагональной) Это в перспективе, конечно, нужно проверять.
Вместо этого далее делается попытка оптимизировать распределение вероятностей на диагональной конфигурации и проверить возможность улучшения за счет этого нижней границы.
Предварительно определим параметры квадрата, расположенного на диагонали и содержащего вершину на главной диагонали с вероятностью

:

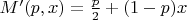
.
Таким образом, подбирая для диагональной конструкции зависимость

и вычисляя параметры
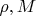
, можно попытаться поднять нижнюю границу.
Чтобы ускорить процесс, я не стал оптимизировать линейные, квадратичные и пр. зависимости, а просто выбрал два «крайних» варианта: 1)

и 2)

, для которых

.
1.

В соответствии с имеющейся нижней границей при

имеем

,т. е.

, значение

ниже границы.
2.

.
В соответствии с имеющейся нижней границей при

имеем

,т. е.

, значение

ниже границы.
Если все-таки имеющаяся нижняя граница неулучшаема, то решение задачи, таким образом, можно свести к следующим этапам: 1)установить факт оптимальности диагональной конструкции и 2)доказать оптимальность для таких конструкций распределения с

.
Рассуждения, формулы и вычисления нужно проверить.



