Можете пояснить, почему этот результат отличается от полученного ранее?
amon взял формулы, как если для рамки без потерь и со сдвинутыми на

щетками относительно их "штатного" положения.

Если производная тока равна синусу, то сам ток равен косинусу, и пики тока попадают на пики верхнего механического уравнения для момента. В нижней формуле синус вместо косинуса означает поворот щеток. А на графике, про который Вы спросили, с установившейся скоростью, совсем другой случай: щетки не сдвинуты, а рамка с потерями

. Это близко к реальному электродвигателю, и эти графики, которые с потерями, я считал контрольными, что программа работает.
В этом сообщении графики, построенные программой-интегратором, которая в сообщении
https://dxdy.ru/post1403194.html#p1403194Здесь рамка без потерь, и щётки сдвинуты на 90 градусов. Привожу новые исходные настройки интегратора, действующие в пределах этого сообщения, а к каждому рисунку буду давать только изменения этих исходных настроек. Под пунктирной чертой выдача программы, но не вся, а только интересная, или совсем без выдачи. На графиках:
Красный - ток рамки, зелёный - угол рамки, синий - скорость, оранжевый - электромагнитный момент.
Исходные настройки:
Код:
// масштаб времени (целые положительные числа)
#define T1 8 // T1>=1. Растяжка времени. На T1 делятся приращения.
#define T2 20000 // сжатие времени на рисунке, на точность не влияет
// Начальные значения
#define I0 0 // Ток
#define A0 -45 // Угол
#define V0 0 // Скорость
#define FI 90 // угол установки шеток. (0 или +90)
// Параметры
#define E0 2 // напряжение батарейки
#define E1 20 // ЭДС-индукции
#define R0 0 // сопротивление потерь
#define M1 0 // момент вязкого трения M=M1*v;
#define M2 0 // момент сухого трения
#define J 9000 // момент инерции, J>0, он в знаменателе
// Размеры рисунка. Можно менять, пошире сделать - больше видно
#define W 600 // ширина
#define H 200 // высота
// Масштабные коэффициенты для графиков
#define AVT 1 // 0 ручная; 1 автоматическая установка кроме T1 и T2
#define K1 0.2 // ток
#define K2 0.9 // угол
#define K3 2 // скорость
#define K4 3 // момент
Рис. 1. Исходные настройки. Это рис. 8 из прошлого моего сообщения. Рамка крутится, но время от времени меняет направление вращения: положительное и отрицательное зелёное на рис.
Код:
---------
t=1500000
Vmax=610.793;

Рис. 2. То же, что рис. 1, но с вязкой нагрузкой и изменён масштаб времени. Обратите внимание, сначала есть вращение, и зелёное достигает максимума, а потом вращения нет, зеленое в узкой полосе (зеленое - это угол рамки).
Код:
#define T2 2000 // сжатие времени
#define M1 2 // момент вязкого трения M=M1*v;
-----------
t=150000
Vmax=10.401;

Рис. 3. То же, что рис. 2, но меньше сжат по времени.
Код:
#define T2 216 // сжатие времени
#define M1 2 // момент вязкого трения M=M1*v;
--------
t=16200
Vmax=10.401;

Рис. 4. Я задал широкий рисунок
16000x200 с малым сжатием времени. Его настройки:
Код:
#define T2 8 // сжатие времени
#define M1 2 // момент вязкого трения M=M1*v;
#define W 16000 // ширина
Из него взял фрагмент, ту часть, где переход с кручения на колебания: график угла (зеленый) перестаёт иметь скачки, угол меняется в диапазоне

. На рисунке сверху чистый фрагмент, а ниже тот же фрагмент, и я подрисовал стрелки - они показывают моменты коммутации при

и

градусах, но при такой большой постоянной составляющей тока эта коммутация уже мало на что влияет. Вернее, влияет на поддержание колебаний, вязкая нагрузка есть.

Голубые полосы сверху указывают промежутки времени, когда рамка в секторе

градусов, при этом положительный ток рамки (а он здесь всюду положительный) даёт отрицательный момент. Что это за провал в середине отрицательного момента под второй и третьей голубыми полосами? А вот что: рамка влетает в голубой сектор на большой скорости и с нулевым моментом, влетает через мертвую точку. Отрицательный момент быстро возрастает и при

достигает максимума, а рамка продолжает двигаться к другой мертвой точке, вот и провал момента. Но не дойдя до другой мертвой точки, рамка меняет знак скорости и движется на выход из голубой зоны, и выходит из неё в ту же сторону, через которую зашла. Короче, первый зубчик момента тормозит влетевшую рамку и не даёт ей перейти вторую мертвую точку, а второй зубчик выталкивает её обратно из голубой зоны.
Ещё один интересный график, по виду схожий с вычисленным "Математикой".
хоть с меандром:
Код:
s6 = NDSolve[{a''[t] == 0.01 i[t] Cos[a[t]], i'[t] == 5 RealSign[Sin[a[t]]] - a'[t] Cos[a[t]], a[0] == 0,a'[0] == 0.1, i[0] == 1}, {a, i}, {t, 0, 2000}]
Plot[Evaluate[{a'[t]} /. s6], {t, 0, 200}, PlotStyle -> Automatic]
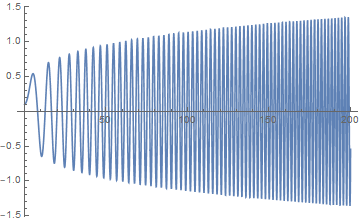
Рис. 5.
Настройки примерно такие, как у
amon. Угол рамки

градус, чтобы не на стыке коллектора. Угол щеток

соответствует сдвигу щеток на

без смены полярности батарейки, т. е. "плюс" перед
5 RealSign[Sin[a[t]]], из-за этого там спорили. Тут соответствует коду от
amon.
Код:
#define T2 24 // сжатие времени
// Начальные значения
#define I0 1 // Ток
#define A0 1 // Угол (градусы)
#define V0 0.2 // Скорость
#define FI -90 // угол установки шеток. (0 или +90)

Рис. 6.
То же, что рис. 5, но сильнее сжато время.
Код:
#define T2 100 // сжатие времени
// Начальные значения
#define I0 1 // Ток
#define A0 1 // Угол (градусы)
#define V0 0.2 // Скорость
#define FI -90 // угол установки шеток. (0 или +90)

У меня появились сомнения, что моя программа-интегратор работает не правильно, по крайней мере на большом времени. Но об этом я напишу потом, а то мне никогда не закончить сообщение.