Большое спасибо всем участникам дискуссии, очень помогли советы и ссылки.
Последняя ссылка
http://matlab.exponenta.ru/mu_analys/book2/1_6.php очень помогла. Большое спасибо, Евгений.
Рассмотрим матрицу
 Лемма 1.
Лемма 1. Спектр

матрицы Z симметричен относительно мнимой оси.
Утверждение леммы сразу следует из равенства
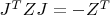
, где

,
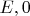
-- матрицы размера
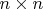
.
Предположение 1. Матрица Z не имеет чисто мнимых собственных значений.При сделанном предположении инвариантное пространство матрицы, назовем его

, соответствующее собственным значениям

с отрицательной вещественной частью

-мерно.
Это пространство есть сумма корневых пространств для собственных чисел с отрицательной вещественной частью.
Существует ортогональная матрица
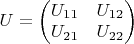
, т.ч. вектора-столбцы матрицы

являются ортогональным базисом пространства

, а остальные вектора-столбцы матрицы

дополняют первые

до ортогонального базиса всего пространства. (Все матрицы
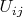
имеют размеры

.)
Тогда имеет место равенство

, где

совпадает с левой от мнимой оси частью
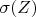
.
Предположение 2. Матрица Z такова, что пространство  содержит ровно один вектор с первыми
содержит ровно один вектор с первыми  нулевыми координатами.
нулевыми координатами.Этот вектор и все остальные координаты имеет нулевые

Предположение 2 эквивалентно требованию обратимости матрицы

.
Лемма 2. Матрица
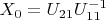
является решением уравнения Риккати.
Доказательство леммы 2. Легко проверить, что имеет место равенство

.
Тогда
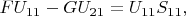

Домножим каждое из этих уравнений справа на

получим


Теперь домножим первое уравнение на

слева и вычтем из него второе:

Правая часть полученного уравнения равна 0.
Лемма 2 доказана.Осталось доказать симметричность матрицы

, а также её положительную полуопределенность.
Лемма 3. Матрица
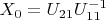
является симметричной и имеет место неравенство

.
Доказательство леммы 3. Рассмотрим функцию
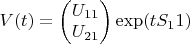
, а также

, где

. В силу того, что

расположен левее мнимой оси, обе этих функции со всем производными при
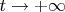
стремятся к 0.
Заметим, что

. Тогда

.
Значит
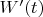
симметрична и выполнено неравенство

.
Так как
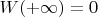
, то получается, что

- симметрично и

.
Но

, а тогда

.
Следовательно, матрица

является симметричной и имеет место неравенство

.
Лемма 3 доказана.-- Пн июл 08, 2019 21:31:17 --Остался вопрос:
Что потребовать от матриц матрицы

, чтобы предположения 1 и 2 выполнялись, и при этом условия были достаточно общими и легко проверяемыми?