найти число, оканчивающееся на цифру пять, большее пяти, представимое разностью квадратов только один раз.
Ну, и задачка. Если такое число не существует, то как это доказать.
Похоже, что она не из простейших,
Коль до сих пор такая тишина.
Я жду совета славных и мудрейших,
Но голова иным у них полна.
Ладно (эту задачу проехали; может она и простая, но я этого не вижу). Тогда в качестве иллюстрации основного наблюдения приведу, действительно, простейшую задачу.
Задача.
Доказать, что количество решений

в положительных натуральных числах (обозначение

) уравнения

больше одного при любом натуральном

.
1). Здесь имеется очевидное решение

при любом

. Т.е., по крайней мере, одно решение существует.
2). Возможные наборы последних цифр левой и правой части уравнения (повторяющиеся цифры учитываются один раз; порядок следования не важен) совпадают.
3). Количество решений

(т.е., по крайней мере существует ещё одно решение

при любом

, которое легко находится).
Вопрос: существует ли контрпример, обладающий свойствами пунктов

и не обладающий свойством пункта

.
Замечание: в качестве используемых операций возможны сложение, умножение и обратные.
-- 08.07.2019, 11:26 --Замечание к уравнению (

).
Мне это уравнение удалось только свести к решению уравнения

,

нечётное,

чётное. Далее, если элементарно, у меня не получается (решение посложнее мне известно).
Противоположный случай, когда

чётное,

нечётное, я доказывала методом матиндукции плюс ограниченный перебор (надо будет проверить, есть ли ошибки в таком подходе). (Очевидно, что чётность должна быть противоположной.)
Поскольку для существования решения исходного уравнения, необходима нечётность
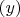
, то второй случай, который мне показался сложным, просто отпадает. Остаётся проверить, нет ли ошибок в доказательстве матиндукцией первого случая.
Если ошибок нет, то метод можно применить для остальных

с небольшой модификацией.