Делимость простых чисел

[Unknown_reader]

Здравствуйте! Встретился с задачей, которая кажется тривиальной на первый взгляд, но понять некоторые тонкости решения я так и не смог. Задача звучит так:

Докажите, что $p^2 - q^2$ делится на 24, если p и q – простые числа, большие 3.

А ее "официальное" решение так:

$p^2 - q^2 = (p - q)(p + q)$. $p - q$ и $p + q$ – чётные числа, причём их разность 2q не кратна 4. Значит, одно из этих чисел делится на 4.
2q также не кратно 3, значит, $p - q$ и $p + q$ дают разные остатки при делении на 3. Если бы ни одно из этих чисел не было кратно 3, то сумма
$(p - q) + (p + q) = 2p$ делилась бы на 3. Но это не так.
Поэтому $(p - q)(p + q)$ делится на $2\cdot4\cdot3 = 24$.

Я на практике доказал что если разность $p - q$ и $p + q$ которая равняется 2q - не делится на 4, значит только одно из этих четных чисел делится на 4. Но мне решительно не понятно почему, если 2q не кратно 3 значит $p - q$ и $p + q$ дают разные остатки при делении на 3. И почему Если бы ни одно из этих чисел не было кратно 3, то сумма
$(p - q) + (p + q) = 2p$ делилась бы на 3. Буду признателен если поможете разобраться! Спасибо!

[Connector]

Unknown_reader в сообщении #1402669 писал(а):

И почему Если бы ни одно из этих чисел не было кратно 3, то сумма
$(p - q) + (p + q) = 2p$ делилась бы на 3.

Это действительно непонятно. Более того, в общем случае это не так.

Но здесь все дело в том, что если оба числа не кратны $3$ и при этом дают разные остатки, то неизбежно эти остатки равны $1$ и $2$ (и сумма чисел кратна $3$).
С первым вопросом все ещё проще.

[Unknown_reader]

Connector в сообщении #1402678 писал(а):

Unknown_reader в сообщении #1402669 писал(а):

И почему Если бы ни одно из этих чисел не было кратно 3, то сумма
$(p - q) + (p + q) = 2p$ делилась бы на 3.

Это действительно непонятно. Более того, в общем случае это не так.

Тут p и q - простые числа больше 3, может это играет?

[SiberianSemion]

Unknown_reader в сообщении #1402669 писал(а):

Но мне решительно не понятно почему, если 2q не кратно 3 значит $p - q$ и $p + q$ дают разные остатки при делении на 3.

Если бы они давали одинаковые остатки, то их разность $2q$ делилась бы на $3.$

Unknown_reader в сообщении #1402669 писал(а):

И почему Если бы ни одно из этих чисел не было кратно 3, то сумма
$(p - q) + (p + q) = 2p$ делилась бы на 3.

Возможные остатки при делении на $3$ - это $0, 1, 2.$ Так как мы установили, что числа дают разные остатки, то выбор ситуаций у нас невелик, и можно их всех перебрать. Точнее, перебрать один)

(Оффтоп)

это как бы если у попа были не чётки, а чета.

[Dendr]

Мудреное какое-то доказательство. Можно проще.

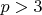
Пусть дано простое $p>3$. Рассмотрим число $p^2-1=(p-1)(p+1)$. Так как $p$ не равно ни 2, ни 3, одно из чисел $p-1$ и $p+1$ кратно 3, и оба они четны. Причем одно из них (не обязательно то же самое) кратно также 4. Таким образом, их произведение делится на $3\cdot 2\cdot 4=24$.
Следовательно, (1) квадрат любого простого числа либо равен единице по модулю 24, либо равен 4 или 9, но эти случаи отброшены из рассмотрения в задаче.
Тогда разность квадратов простых чисел, больших 3, всегда делится на 24.

Утверждение (1) можно также доказать, воспользовавшись тем, что любое простое число (кроме 2 и 3) представимо в виде $6n\pm 1$