в п. 1) предполагается перебор пар

при условиях
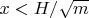
,

и проверка выполнения равенства

. Так?
Да, так.
2). Остаётся рассмотреть

.
Покажем, что тогда
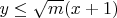
.
Здесь, в случае знака равенства в неравенстве, будем иметь уравнение от одной переменной (простой случай; я его не рассматриваю).
При

получим

. Т.е. в итоге
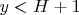
для

доказательство верно?
Далее, по второму пункту будем считать, что доказана необходимость неравенства (знак равенства в нём пока не рассматриваем, т.к. это просто)

при
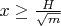
.
Для существования решения необходимо выполнение условия

. Тогда, с учётом необходимости неравенства, доказанного выше, необходимо выполнение неравенства
Здесь решили неравенство относительно переменной

. Из последнего неравенства следует, что

при
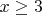
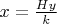
подставляем в исходное уравнение. Получим

Знаменатель должен быть больше нуля. Т.е.
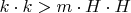
. Т.к.

то должно быть

, чтобы выполнялось условие положительности знаменателя. Получаем, что натуральная переменная

может принимать только ограниченное количество значений, заключённых в диапазоне
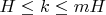
. Т.е. имеем не уравнение, а серию равенств, которые должны выполняться (правая часть должна быть полным квадратом). Вот и проверяем их. Здесь, хотя переменная

неограниченная, но

ограниченная. Поэтому перебор ограничен. Если равенство выполняется при некотором значении

, то получаем после подстановки

в исходное уравнение уравнение от одной переменной
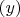
(это просто; не рассматриваю).



