Я понимаю, что все это выглядит как жонглирование определениями, но как тогда вообще определяются различные числовые множества?
Кстати, определить множество — не значит предъявить некоторую запись

. Такой записи может не соответствовать множества; например,

(где выражение справа — это просто сокращение некоторого длинного, но точно описываемого предиката) множества не определяет, оно «слишком большое». Чтобы такая запись определяла множество, надо чтобы оно подходило под одну из аксиом существования. Плюс, многие из таких аксиом дают нам другие записи, в которые если подставить множества, они дадут множество: например, задание конечным перечислением элементов

, или
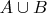
(и вообще объединение произвольного семейства множеств), или
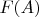
— образ множества

при отображении

, или ещё некоторые. Хотя вот аксиома выделения как раз даёт нам использовать любую запись вида
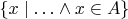
, где

уже известное множество.
Ещё надо заметить, что запись
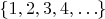
ничего конкретного не определяет. Недалёким от истины будет считать, что

даётся нам аксиоматически (на деле постулируется некоторое его надмножество, не обязательно даже единственное, но из них можно однозначно вытащить

).
Всё вышесказанное — об аксиомах ZFC, но обычно на этом не фиксируются, если не изучают конкретно теорию множеств саму по себе. Можете считать, что есть некоторая кучка конструкций, которая даёт множества, если в них использовать ранее определённые множества, и её часто достаточно взять довольно узкой. Декартово произведение множеств и упорядоченные пары (и далее,

-ки) тоже вполне разумно включить в такой набор и не особо думать об основаниях.