Решил внять Вашему
vpb совету, и опробовать алгоритм с регулируемым

. Вот такой:

Стратегию изменения

, для начала, выбрал самую простую, изначально предложенную Марквардтом [Демиденко Е.З. Линейная и нелинейная регрессии. М.: Финансы и статистика, 1981. -С. 254.], а именно - некоторое начальное

на каждой итерации уменьшается в несколько раз. Если, после этого функционал не убывает -

увеличивается, до тех пор, пока не будет достигнуто убывание. В указанном выше источнике коэффициент уменьшения и коэффициент увеличения

равны 10, а начальное значение берётся 0.01. Вычисления показывают, что при этих значениях, на моей задаче, наблюдается такое же "застревание" как и в алгоритме с дроблением шага. При этом

стремится к бесконечности и алгоритм останавливается, не достигнув минимума целевой функции.
Я использовал коэффициент дробления

и коэффициент увеличения

, начальное значение оставил таким же (оказалось, что оно мало на что влияет). В алгоритма Марквардта используется пропорциональный регуляризатор, т.е. вместо единичной матрицы, в алгоритме используется диагональ

. Встречал в разных источниках различные описания преимуществ данного подхода. Однако, у меня, всё получилось, с точностью до наоборот. Пропорциональный регуляризатор оказался хуже. Алгоритм с ним сходится быстрее только на начальном этапе, а потом, скорость сходимости сильно замедляется. Хуже всего - с ним алгоритм более склонен "застреванию". Его работа так же существенно зависит от выбора начального

.
С прямым же регуляризатором удалось добиться более-менее устойчивой работы алгоритма. Вычисления показывают, что теперь, он сходится от самых разных начальных приближений. Кривая сходимости всегда примерно одинаковая, и имеет следующий вид
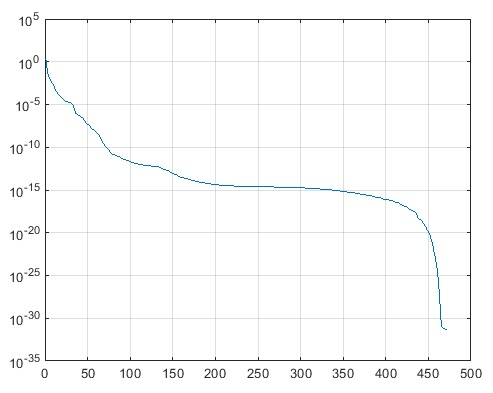
При достижении предела вычислительной точности

очень быстро возрастает до

. Поэтому, мне показалось очень удобным использовать следующий критерий останова:

.
Так же выяснился один нюанс - точность процедуры обращения матрицы здесь очень важна. У меня используется весьма трудоёмкая процедура псевдообращения, на основе сингулярного разложения. Попытка замены этой процедуры прямым алгоритмом решения СЛАУ, на основе LU разложения, приводит к полной потере работоспособности. Наверное, это актуально только для больших, плохо обусловленных матриц.
Разумеется, надо будет попробовать более совершенные стратегии подбора

, описанные в книге Дэннис-Шнабель, а так же - использовать полную матрицу Гессе.
Вообще, конечно, сходится полученный алгоритм не так быстро, как хотелось бы. Тем более, что задача была выбрана специально небольшая.
Но это уже кое что! Надеюсь, в дальнейшем получиться его улучшить.
Большое спасибо Вам
vpb, за помощь



