Найти: ряд распределения; FX (x); M[X]; D[X];

[DifferentKf]

Здравствуйте! У меня возникли трудности с данной задачей:
В урне лежат 2 шара – черный и белый.
Если извлекаемый шар оказывается белым, то он возвращается в урну и добавляются еще 2 белых шара.
Извлекают по одному шару до появления черного, но не более 5-ти раз; случайная величина $X$ – количество извлечений.
Найти: ряд распределения; $FX (x); M[X]; D[X];$ $\sigma$_{X} $
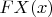
Изобразить ряд распределения и $FX (x)$ на графике.

Моё примерное решение, но не уверен, что правильное:

$\begin{tabular}{|l|l|l|l|l|l|} \hline x & 1 & 2 & 3 & 4 & 5 \\ \hline m_{i} & 2 & 4 & 6 & 8 & 10 \\ \hline p_{i} & $\frac{1}{2} & $\frac{1}{4} & $\frac{1}{6} & $\frac{1}{8} & $\frac{1}{10}$ \\ \hline \end{tabular}$

$M[X] = 1 \cdot \frac{1}{2} + 2 \cdot \frac{1}{4} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{8} + 5 \cdot \frac{1}{10}= 2,5$

$D[X] = \frac{1}{2} + 1 + \frac{9}{6} + \frac{16}{8} + \frac{25}{10} = 7,5 \Rightarrow 7,5-6,25 = 1,25$

$M =\frac{0,5 + 0,25 + 1/6 + 1/8 + 1/10}{10} = \frac{1}{2} + \frac{1}{4} + \frac{1}{6} + \frac{1}{8} + \frac{1}{10} =\frac{550 + 135}{600} = \frac{685}{600} = 1\frac{85}{600} = 1 \frac{17}{120} = \frac{137}{1200} \approx 0,11417$

$\sigma(x) \approx 1,118$

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы): отдельные обозначения (в том числе и внутри таблицы) тоже нужно оформить как формулы, внутри формулы не должно быть долларов, только по краям.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.