Книга: "ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ ДЛЯ ТЕХНИКУМОВ", И. Л. Зайцев, Москва, 1972 год. Вот задача номер 21:

Пардон за плохое качество картинки, это веб-камера, лучше нету. А вот мой рисунок к задаче, а решения я напишу в Латехе ниже под рисунком:

Исходя из того, что окружность и гипербола может быть описана в удобных, собственных координатах (мы отбрасываем случай когда центр окружности не совпадает с центром собственных координат гиперболы и собственно гиперболы), и исходя с сути тангенса касаемых гиперболы, сразу запишем что:

поскольку мы знаем что радиус окружности в этих, удобных координатах будет три, и что радиус окружности также является малой полуосью гиперболы, можем заключить что большая полуось гиперболы, оно же мнимая, будет

соответственно каноническое уравнение гиперболы будет что-то вроде этого

или


делим обе стороны равности на девять

а ответ в книге:
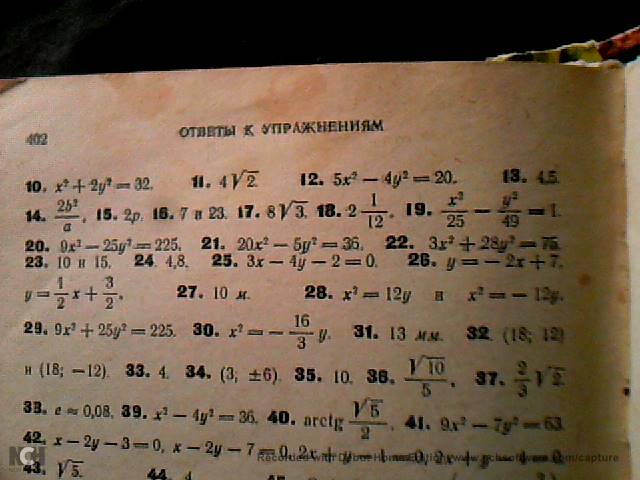
То есть одна часть "весов" уравнения совпадает с моим ответом, а вторая, ну никак, я не знаю какими математическими преобразованиям превратить свой ответ в книжный, может я где-то, сонными глазами/разумом, как говорится напартачил... Но вообще не знаю. Не ну можно попробовать додумать типо мы это все в каких-то других координатах рассматриваем, в таких где вот окружность центром находиться в центре этих координат, а гипербола со своим центром, соответственно нет, но моя интуиция подсказывает что автор не усложнял бы так, все таки книга хоть старая (в старых все усложняли, походу делались для учеников что там та мат-кружки ходили и все такое), но все-же для техникумов.



