Помогите разобраться в одном неравенстве из доказательства оценки сложности алгоритма Карацубы.
В известной книге J. von zur Gathen, J.Gerhard "Modern Computer Algebra" (
https://www.twirpx.com/file/1252085/)
в Лемме 8.2 доказывается оценка сложности для рекурсивных алгоритмов некоторого типа, под который подпадает, в частности, алгоритм Карацубы.
В частности, в первом пункте доказательства выводится следующее промежуточное неравенство к которому нет вопросов:

, если
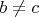
,

где

есть положительные вещественные числа, логарифм берется по основанию 2, а T и S есть функции из натуральных чисел в натуральные числа.
Далее показывается, что

,

Тогда, пользуясь неравенством (2), можно перейти от неравенства (1) к следующему неравенству (3):

, если

, (3)
А теперь, собственно, шаг, который и вызывает вопрос - далее авторы переписывают неравенство (3) в виде следующего неравенства (4):

, если

, (4)
Вопрос - а куда делся при выносе за скобки

множитель

при

?
При

, неравенство (4), действительно, следует из (3) ( в формулах,

есть степень 2).
Но при

, мы же не можем так просто отбросить множитель

. В чем тут дело ? Спасибо.