К сожалению, никто не заинтересовался решением этой простой задачки.
Итак, будем доказывать, что если составить таблицу Кэли по операции умножения остатков (исключая нуль) от деления по модулю простого числа
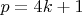
, то сумма элементов обеих диагоналей равна

.
1. Поскольку число

простое, то в каждой строке и каждом столбце стоят все различные числа от 1 до (p-1).
2. На главной диагонали стоят все вычеты, сравнимые с

, где

пробегает числа от 1 до (p-1), т.е. там стоят все квадратичные вычеты по модулю p. Поскольку квадратичных вычетов ровно

, а

, то на главной диагонали удвоенное количество квадратичных вычетов. Если

- квадратичный вычет простого числа
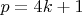
, то и

- квадратичный вычет, т.е. в свою очередь квадратичные вычеты можно сгруппировать по парам, так чтобы их сумма равнялась

. Таким образом, сумма чисел главной диагонали - это

3. Во второй диагонали находятся произведения

, т.е. ясно, что там тоже стоят квадратичные вычеты, на которые можно распространить теже самые рассуждения.



